Chamamos de Movimento Harmônico Simples (MHS) todo movimento que descreve uma trajetória linear que oscila periodicamente em torno de uma posição de equilíbrio. Um bom exemplo é imaginar uma mola pendurada com uma determinada massa presa na ponta. Essa mola está parada, em equilíbrio, e quando a puxamos e ela começa a oscilar. Nessa oscilação, imaginando que estava no vácuo, livre de resistências, ao soltar a massa, esta vai subir, passar pelo ponto de equilíbrio, subir mais um pouco e descer. Na descida, vai passar novamente pelo ponto de equilíbrio, parar instantaneamente no ponto onde foi solta e voltar ao movimento de subida.
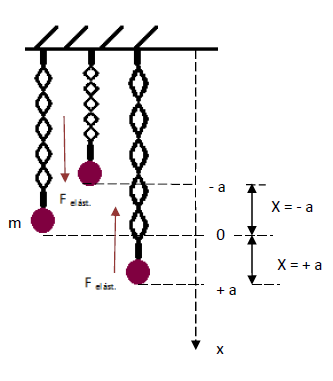
A distância que a massa se move até o ponto de equilíbrio chama-se amplitude. No caso do desenho acima, a amplitude do sistema é a (em módulo). Nestes pontos extremos (+a e –a) inverte-se a orientação do movimento e, portanto, a velocidade é nula. Então, a velocidade volta a aumentar até ter seu valor máximo (também em módulo) no ponto de equilíbrio (x = 0).
Como o MHS pressupõe periodicidade, ou seja, um ciclo que sempre se repete no mesmo intervalo de tempo, usamos o conceito de período T para descrevê-lo.
“Período: intervalo de tempo de um ciclo. Por exemplo, o ponteiro que marca os segundos tem um período de 60s porque nesse intervalo de tempo ele completa um ciclo – e inicia outro. ”
O período o MHS é determinado pela massa que se prende à mola e pela constante elástica k da mesma.
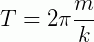
Perceba que o período do MHS não depende da amplitude que a mesma desenvolve. A amplitude está relacionada à energia potencial elástica (Epelást.) cedida ao sistema (o quanto a mola foi esticada ou comprimida para iniciar seu movimento). Quando em MHS, o sistema tem energia potencial elástica (associada a restauração da mola para seu ponto de equilíbrio) e energia cinética (Ec) pois a massa tem velocidade durante o movimento. Essa energia é dada por:
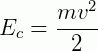
E_\text{pelást}=\frac{kx^2}{2}[/latex]
A associação dessas energias resulta na energia mecânica (Emec.) do sistema:
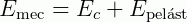
No MHS, o corpo muda sua posição, distância em relação ao ponto de equilíbrio enquanto também muda sua velocidade. Assim, percebemos que a energia mecânica do sistema é constante enquanto suas energias constituintes (cinética e elástica) oscilam entre si.
Assim, podemos concluir que quando o sistema tem amplitude máxima, a energia cinética é nula – como falamos acima, é o ponto de inversão do movimento, quando o sistema tem velocidade zero. Do mesmo modo, quando o sistema passa pelo ponto de equilíbrio, e tem velocidade máxima, sua energia potencial elástica é nula pois neste momento, a mola não está deformada.
Texto originalmente publicado em https://www.infoescola.com/fisica/movimento-harmomico-simples-mhs/