Princípio de Fermat

Em agosto de 1657, o matemático francês Pierre Fermat (1601-1665) escreveu uma carta (Epistolae 42) a Monsieur Cureau de la Chambre, na qual enunciou o seu famoso Princípio do Tempo Mínimo: A Natureza sempre escolhe os menores caminhos.

De acordo com esse princípio, Fermat descreve a trajetória de propagação da luz pelo seguinte conceito:

“A trajetória seguida pela luz viajando de um ponto a outro é tal que o tempo de viagem é o mínimo. Isto é, a luz percorre a trajetória mais rápida.”

O fato de a trajetória ter uma menor distância não quer dizer que ela é necessariamente a trajetória de menor tempo.

Por exemplo, considere que há dois caminhos de chegar a uma cidade, no caminho A seria necessário dirigir 30 km por uma estrada de terra irregular com uma velocidade máxima de 40 km/h e no caminho B seria necessário dirigir 50 Km por uma estrada asfaltada a uma velocidade máxima de 100 Km/h. A estrada A tem o menor percurso mas você chegará primeiro passando pela estrada B, o mesmo ocorre com a luz - ela procura a trajetória que apresenta o melhor meio para percorrer.

O tempo para realizar o percurso é dado pelo somatório de tempo percorrido em cada meio:

$t = \sum_{i=1}^{N} t_i$

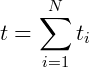
Onde 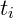$t_i$ é o tempo para percorrer em cada meio.

Sabendo que 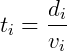$t_i = \frac{d_i}{v_i}$ e que a velocidade do meio (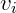$v_i$) é o índice do meio (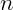$n$) dividido pela a velocidade da Luz (c) chegamos à equação:

$t = \frac{1}{C} \sum_{i=1}^{N} n_i d_i$

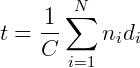
Usando um conceito a nível superior podemos encontrar o tempo utilizando à integral:

$t = \displaystyle\int_A^B \; \frac{n}{c} \cdot ds = \displaystyle\int_A^B \; \frac{ds}{v}$

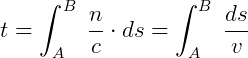
Onde:

• ds - é um elemento infinitésimo de comprimento.
• A - é o inicio da trajetória da luz
• B - é o fim da trajetória da luz

Leis de reflexão e refração da luz

As leis da reflexão e refração da luz se derivam do principio de Fermat.

Lei da reflexão

Usando o principio de Fermat podemos confirmar a seguinte lei da reflexão.

“O ângulo de incidência é igual o ângulo de reflexão.”

Dedução da lei

Raio de luz refletindo em um espelho

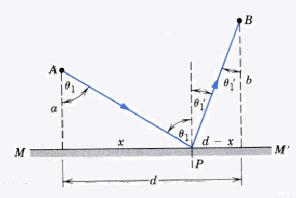
O caminho ótico de A para B é dado pela distancia AP mais a distancia PB. Podemos calcular essa distancia (P) utilizando o teorema de Pitágoras.

$P = \sqrt{a^2 + x^2} + \sqrt{b^2 + (d - x)^2}$

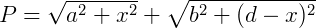
O principio de Fermat diz que a distancia deve ser mínima, para descobrir a menor distancia, o menor valor de x, derivamos a equação e igualamos a zero.

$\frac{dP}{dx} = \frac{x}{\sqrt{a^2 + x^2}} - \frac{d - x}{\sqrt{b^2 + (d -x)^2}} = 0$

$\frac{x}{\sqrt{a^2 + x^2}} = \frac{d - x}{\sqrt{b^2 + (d - x)^2}}$

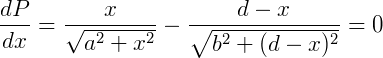
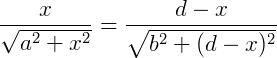
Sabendo que Sen Ѳ = cateto oposto / hipotenusa.

Concluímos que Sen Ѳ = Sen Ѳ1

Lei da refração

Usando o principio de Fermat podemos confirmar a seguinte lei da refração.

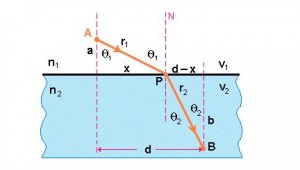
Quando a luz passa de um meio, cujo índice de refração n1, para outro meio cujo índice de refração é n2,tem sempre N1 sen Ѳ = n2 sen Ѳ1

Dedução da lei

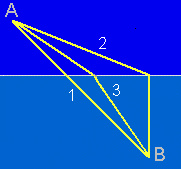
Na figura a seguir, foi ilustrado 3 trajetórias  diferentes para a luz percorrer do ponto A ao ponto B (devemos lembrar que existem  infinitas trajetórias).

Possíveis trajetórias para um raio luminoso refratado

Como a luz ira percorrer por dois meios distintos, por exemplo, ar e vidro, ela tente a percorrer a maior distancia no meio onde a sua velocidade é maior, dessa forma ela “economiza” tempo chegando ao ponto B mais rápido.

Refração

O tempo para percorrer o trajeto AB é igual à soma de AP com PB, sabendo que o tempo é dado pela distancia dividida pela velocidade. Encontramos que o tempo total é:

$t = \frac{r_1}{v_1} + \frac{r_2}{v_2}$

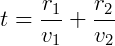
Considerando que v = c/n e o teorema de Pitágoras temos:

$t = \frac{r_1}{v_1} + \frac{r_2}{v_2} = \frac{n_1 \cdot r_1}{c} + \frac{n_2 \cdot r_2}{c} = \frac{1}{c} \cdot (n_1 \cdot r_1 + n_2 \cdot r_2) =$

$= \frac{1}{c} \cdot \left( n_1 \cdot \sqrt{a^2 + x^2} + n_2 \cdot \sqrt{b^2 + (d - x)^2} \right)$

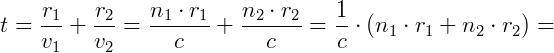
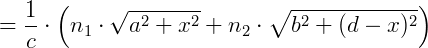
Derivando e igualando a zero para achar o valor mínimo de x encontramos:

$\frac{dt}{dx} = \frac{1}{c} \left[ \frac{n_1 x}{\sqrt{a^2 + x^2}} - \frac{n_2 (d-x)}{\sqrt{b^2 + (d-x)^2}}\right]$

$\frac{n_1 x}{\sqrt{a^2 + x^2}} = \frac{n_2 (d-x)}{\sqrt{b^2} + (d-x)^2}$

$n_1 \cdot sen \theta_1 = n_2 \cdot sen \theta_2$

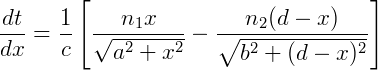
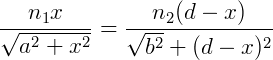
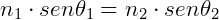
Bibliografia:
Tipler Paul;Mosca,Gene. Física para cientista e Engenheiros  vol 2 , 6º ed ,editora LTC, Rio de Janeiro ,2009.

https://web.archive.org/web/20100730052205/http://vsites.unb.br:80/iq/kleber/CursosVirtuais/QQ/aula-3/aula-3.htm acessado em 20/03/2011
http://efisica.if.usp.br/otica/universitario/raios/fermat/ acessado em 18/03/2011

Texto originalmente publicado em https://www.infoescola.com/fisica/principio-de-fermat/