Adição e subtração de Matrizes - Matemática

Adição e subtração de matrizes é uma operação bem simples a ser feita. Claro que para melhor compreensão do leitor sobre este tema, recomendamos a leitura do artigo sobre Matrizes.

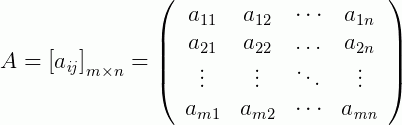
Já sabemos que uma matriz A, de uma forma geral, pode ser representada por:

$A={\left\lbrack {a}_{\mathit{ij}}\right\rbrack }_{m\times n}=\left(\begin{array}{c}{a}_{11}\\{a}_{21}\\\vdots \\{a}_{m1}\end{array}\begin{array}{c}{a}_{12}\\{a}_{22}\\\vdots \\{a}_{m2}\end{array}\begin{array}{c}\cdots \\\dots \\\ddots \\\cdots \end{array}\begin{array}{c}{a}_{1n}\\{a}_{2n}\\\vdots \\{a}_{\mathit{mn}}\end{array}\right)$

Onde 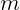$m$ é o número de linhas e n o número de colunas de uma matriz. Note que o elemento 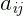${a}_{\mathit{ij}}$ , também chamado de ij-ésima entrada simboliza a posição deste elemento dentro da matriz, ou seja, 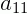${a}_{11}$ está posicionado na 1ª linha e na 1ª coluna. O 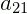${a}_{21}$ está na 2ª linha e na 1ª coluna e assim por diante.

Para que seja possível a soma ou a subtração de duas matrizes, por exemplo, A e B, é necessário que elas possuam a mesma dimensão (ou ordem), ou seja, o número de linhas e de colunas de A devem ser os mesmos de B. Vamos escrever esta soma de um modo geral:

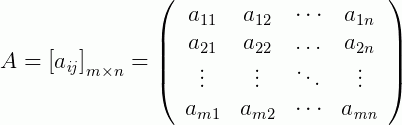
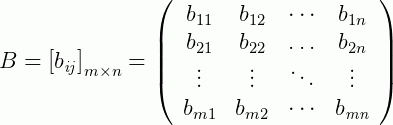
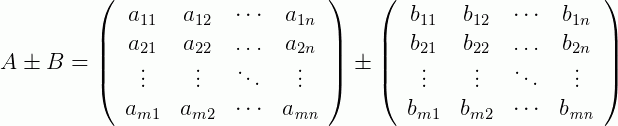
$B={\left\lbrack {b}_{\mathit{ij}}\right\rbrack }_{m\times n}=\left(\begin{array}{c}{b}_{11}\\{b}_{21}\\\vdots \\{b}_{m1}\end{array}\begin{array}{c}{b}_{12}\\{b}_{22}\\\vdots \\{b}_{m2}\end{array}\begin{array}{c}\cdots \\\dots \\\ddots \\\cdots \end{array}\begin{array}{c}{b}_{1n}\\{b}_{2n}\\\vdots \\{b}_{\mathit{mn}}\end{array}\right)$

$A\pm B=\left(\begin{array}{c}{a}_{11}\\{a}_{21}\\\vdots \\{a}_{m1}\end{array}\begin{array}{c}{a}_{12}\\{a}_{22}\\\vdots \\{a}_{m2}\end{array}\begin{array}{c}\cdots \\\dots \\\ddots \\\cdots \end{array}\begin{array}{c}{a}_{1n}\\{a}_{2n}\\\vdots \\{a}_{\mathit{mn}}\end{array}\right)\pm \left(\begin{array}{c}{b}_{11}\\{b}_{21}\\\vdots \\{b}_{m1}\end{array}\begin{array}{c}{b}_{12}\\{b}_{22}\\\vdots \\{b}_{m2}\end{array}\begin{array}{c}\cdots \\\dots \\\ddots \\\cdots \end{array}\begin{array}{c}{b}_{1n}\\{b}_{2n}\\\vdots \\{b}_{\mathit{mn}}\end{array}\right)$

Agora, a soma ou a subtração das matrizes será obtida somando (ou subtraindo) os elementos correspondentes de A e de B, ou seja:

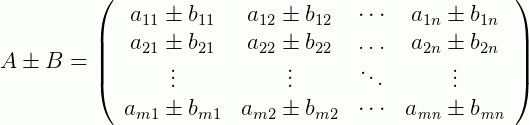
$A\pm B=\left(\begin{array}{c}{a}_{11}\pm {b}_{11}\\{a}_{21}\pm {b}_{21}\\\vdots \\{a}_{m1}\pm {b}_{m1}\end{array}\begin{array}{c}{a}_{12}\pm {b}_{12}\\{a}_{22}\pm {b}_{22}\\\vdots \\{a}_{m2}\pm {b}_{m2}\end{array}\begin{array}{c}\cdots \\\dots \\\ddots \\\cdots \end{array}\begin{array}{c}{a}_{1n}\pm {b}_{1n}\\{a}_{2n}\pm {b}_{2n}\\\vdots \\{a}_{\mathit{mn}}\pm {b}_{\mathit{mn}}\end{array}\right)$

Vamos apresentar um exemplo simples. Dadas duas matrizes:

$A=\left(\begin{array}{cc}1& 2\\3& 4\end{array}\right)$

$B=\left(\begin{array}{cc}5& 6\\7& 8\end{array}\right)$

$A+B=\left(\begin{array}{cc}1+5& 2+6\\3+7& 4+8\end{array}\right)=\left(\begin{array}{cc}6& 8\\10& 12\end{array}\right)$

$A-B=\left(\begin{array}{cc}1-5& 2-6\\3-7& 4-8\end{array}\right)=\left(\begin{array}{cc}-4& -4\\-4& -4\end{array}\right)$

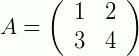
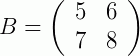
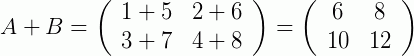
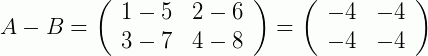
Outro exemplo, agora para a soma de duas matrizes linha:

$A=\left(\begin{array}{ccc}2& -3& 5\end{array}1\right)$

$B=\left(\begin{array}{ccc}1& 4& 2\end{array}0\right)$

$A+B=\left(\begin{array}{ccc}2+1& \left(-3\right)+4& 5+2\end{array}1+0\right)=\left(\begin{array}{ccc}3& 1& 7\end{array}1\right)$

$A-B=\left(\begin{array}{ccc}2-1& \left(-3\right)-4& 5-2\end{array}1-0\right)=\left(\begin{array}{ccc}1& -7& 3\end{array}1\right)$

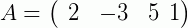
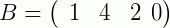
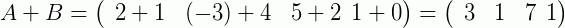
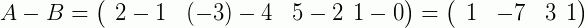
Então, desde que as matrizes nas quais se quer somar ou subtrair possuam a mesma dimensão, basta somar os seus elementos correspondentes. Vamos a mais um exemplo para reforçar:

$A=\left(\begin{array}{ccc}1& 3& 6\\2& 1/2& -5\\-1& 4& 0\end{array}\right)$

$B=\left(\begin{array}{ccc}3& 11& 1\\8& 4& 1\\9& -2& 7\end{array}\right)$

$A+B=\left(\begin{array}{ccc}1+3& 3+11& 6+1\\2+8& \left(1/2\right)+4& \left(-5\right)+1\\\left(-1\right)+9& 4+\left(-2\right)& 0+7\end{array}\right)=\left(\begin{array}{ccc}4& 14& 7\\10& 9/2& -4\\8& 2& 7\end{array}\right)$

$A-B=\left(\begin{array}{ccc}1-3& 3-11& 6-1\\2-8& \left(1/2\right)-4& \left(-5\right)-1\\\left(-1\right)-9& 4-\left(-2\right)& 0-7\end{array}\right)=\left(\begin{array}{ccc}-2& -8& 5\\-6& -7/2& -6\\-10& 6& -7\end{array}\right)$

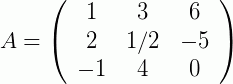
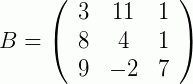
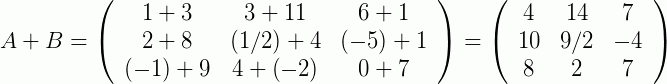
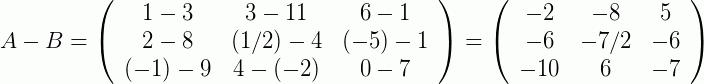
Propriedades da Soma de Matrizes:

Sejam A, B e C matrizes quaisquer e de mesmo tamanho e x e y números quaisquer, então valem as propriedades:

1 – 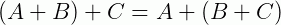$\left(A+B\right)+C=A+\left(B+C\right)$

2 – 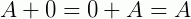$A+0=0+A=A$ , sendo aqui como uma matriz nula com o mesmo tamanho da matriz A

3 – 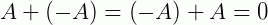$A+\left(-A\right)=\left(-A\right)+A=0$ , onde também é uma matriz nula do mesmo tamanho de A

4 – 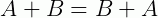$A+B=B+A$

5 – 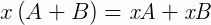$x\left(A+B\right)=\mathit{xA}+\mathit{xB}$

6 – 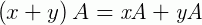$\left(x+y\right)A=\mathit{xA}+\mathit{yA}$

Referências bibliográficas:

ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed. Rio de Janeiro: Elsevier, 2017.

LIPSCHUTZ, Seymor; LIPSON, Marc. Álgebra Linear – 4ª Ed. Porto Alegre: Bookman, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/adicao-e-subtracao-de-matrizes/