Equação do 2º grau em  , na incógnita x, é toda igualdade do tipo:
, na incógnita x, é toda igualdade do tipo:
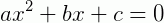
ou redutível a esse tipo, onde a, b e c são números reais e a é não nulo.
A equação é chamada de 2º grau devido à incógnita x apresentar maior expoente igual a 2.
Quando b ≠ 0 e c ≠ 0 (a é sempre não nulo), a equação é chamada de completa.
Se b = 0 e ou c = 0, a equação diz-se incompleta.
Exemplos
1. 3x2 + 4x - 5 = 0 é uma equação de 2º grau completa com a = 3, b = 4 e c = -5.
2. x2 + 5x = 0 é uma equação de 2º grau completa com a = 1, b = 5 e c = 0.
3. 2x2 - 9 = 0 é uma equação de 2º grau completa com a = 2, b = 0 e c = -9.
4. 3x2 = 0 é uma equação de 2º grau completa com a = 3, b = 0 e c = 0.
RESOLUÇÃO DAS EQUAÇÕES INCOMPLETAS
Quando a equação de 2º grau é incompleta, sua resolução é bastante simples. Vamos analisar caso a caso.
1º caso: b = 0 e c = 0; temos então: 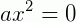
Exemplo
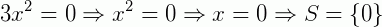
2º caso: c = 0 e b ≠ 0; temos então: 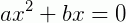
Exemplo
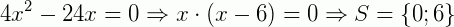
3º caso: b = 0 e c ≠ 0; temos então:
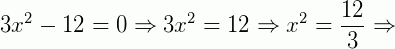
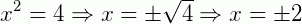
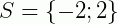
Conteúdo deste artigo
Resolução das equações completas
A resolução da equação completa de 2º grau é obtida através da fórmula que foi demonstrada por Bhaskara, matemático hindu nascido no século XII; por meio da qual sabemos que o valor da incógnita que satisfaz a igualdade é:
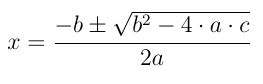
Fórmula de Bhaskara
O número b2 – 4.a.c chama-se discriminante da equação e é representado, geralmente, pela letra grega Δ (delta). Fazendo, então:
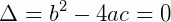
reescrevemos as soluções da equação como segue:
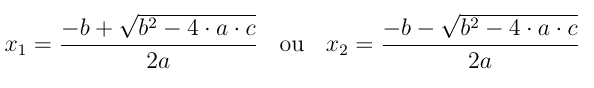
Observação: A fórmula acima só se aplica quando Δ ≥ 0; quando ocorre Δ < 0, a equação não tem soluções reais.
Exemplos
1. Para a equação x2 - 5x + 6 = 0, temos: a = 1, b = -5, c = 6
Portanto: Δ = b2 – 4.a.c = (-5)2 – 4.(1).(6) = 25 – 24 = 1 e as raízes são:
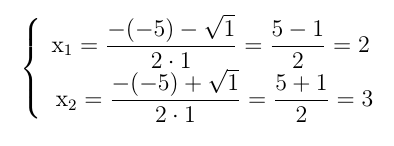
e o conjunto solução é S = {2, 3}
2. Para a equação x2 - 6x + 9 = 0, temos: a = 1, b = -6, c = 9
Portanto: Δ = b2 – 4.a.c = (-6)2 – 4.(1).(9) = 36 – 36 = 0 e as raízes são:
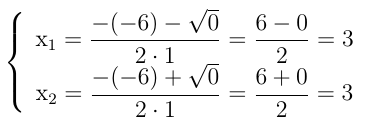
e o conjunto solução é S = {3}
3. Para a equação 3x2 + 4x + 5 = 0, temos: a = 3, b = 4, c = 5
Portanto: Δ = b2 – 4.a.c = (4)2 – 4.(3).(5) = 16 – 60 = -44.
Neste caso, como Δ < 0 a equação não tem soluções reais. Logo, o conjunto solução é 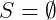 .
.
Equações biquadradas
Equação biquadrada em 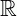 , na incógnita x, é toda igualdade do tipo:
, na incógnita x, é toda igualdade do tipo:
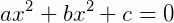
onde a, b e c são números reais e a é não nulo.
Para a resolução das equações biquadradas, usamos de um artifício que as transformam em equações do 2º grau. Veja como é simples: fazemos a substituição:
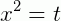
e
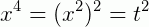
A equação ax4 + bx2 + c = 0 transforma-se, então, em at2 + bt + c = 0, que já sabemos resolver.
Exercícios resolvidos
1º) Resolver a equação x4 - 13x2 + 36 = 0.
Solução
Fazemos:
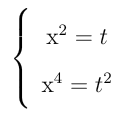
obtendo a equação t2 - 13t + 36 = 0. Para esta última, temos: Δ = b2 – 4.a.c = (-13)2 – 4.(1).(36) = 169 – 144 = 25 e, portanto:
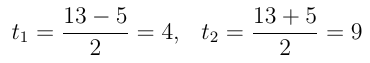
Agora, achamos a incógnita x. Lembrando que x2 = t, vem:
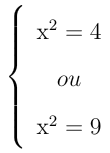 |
⇒ | 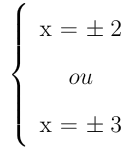 |
Então, o conjunto solução da equação proposta é S = {-3, -2, 2, 3}
2º) Resolver, em 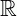 , a equação x4 - 3x2 - 4 = 0.
, a equação x4 - 3x2 - 4 = 0.
Solução
Fazendo a substituição convencional, temos:
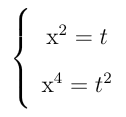
t2 - 3t - 4 = 0
Para esta última, temos: Δ = b2 – 4.a.c
Δ = (-3)2 – 4.(1).(-4) = 9 + 16 = 25 e, portanto:
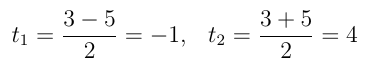
Fazendo a mudança de variável: x2 = t, vem:
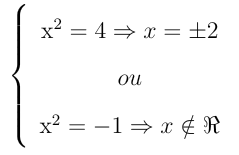
Resolução irracionais
Uma equação é irracional se sua incógnita aparecer sob o sinal de radical (ou elevada a expoente fracionário).
Exemplos
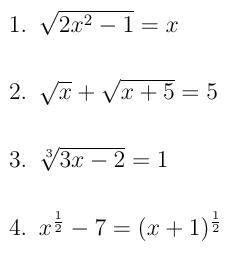
Em seguida, vamos mostrar algumas equações irracionais que podem ser transformadas em equações do 2º grau.
Exercícios resolvidos
1º) Resolver a equação 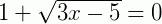
Solução
Isola-se o radical: 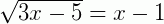
Elevando-se ambos os membros da equação ao quadrado:
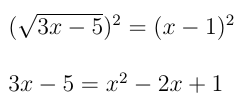
Reduzem-se termos semelhantes e ordena-se a equação, obtém-se:
x2 – 5x + 6 = 0, que possui as raízes: x = 2 ou x = 3
Verificação:
Para x=2, 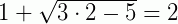 ⇒ 1+1=2 (verdadeiro!)
⇒ 1+1=2 (verdadeiro!)
Para x=3, 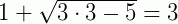 ⇒ 1+2=3 (verdadeiro!)
⇒ 1+2=3 (verdadeiro!)
Portanto, o conjunto solução S = {2, 3}
2º) Resolver a equação 
Solução
Elevando-se ambos os membros da equação ao quadrado:
![]()
2x2 – 1 = x2 ⇒ x2 = 1 , que possui as raízes: x = -1 ou x = +1
Verificação:
Para x=-1, 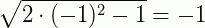 ⇒ falso!
⇒ falso!
Para x=1, 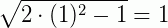 ⇒ verdadeiro!
⇒ verdadeiro!
Portanto, o conjunto solução S = {1}
Texto originalmente publicado em https://www.infoescola.com/matematica/equacao-do-segundo-grau/