Equação fundamental da reta

Quando estudamos função, verificamos que uma função do 1º grau é definida por uma expressão algébrica do 1º grau com duas variáveis que o seu gráfico é uma reta.

Reciprocamente, podemos dizer que uma linha reta é representada por uma equação do 1º grau com duas variáveis.

Neste texto, estudaremos a equação fundamental da reta.

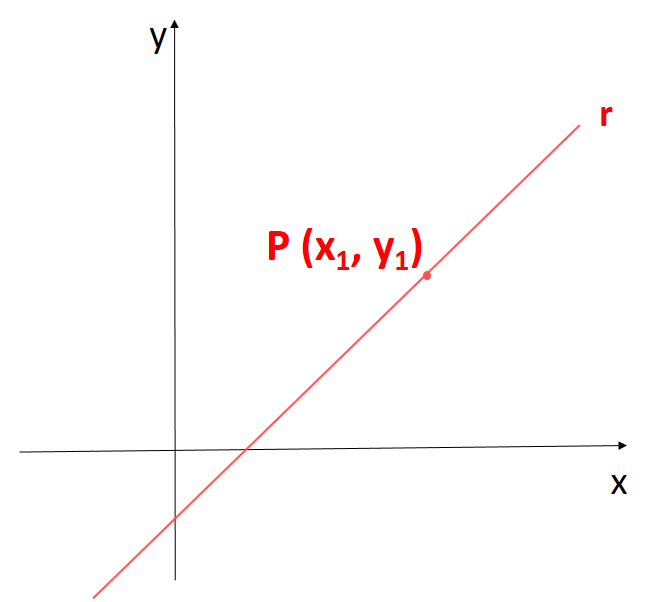
Vamos obter a equação de uma reta que passa por um ponto P(x₁, y₁) e cujo coeficiente angular é m.

Consideremos uma reta r que passa pelo ponto P(x₁, y₁) e tem coeficiente angular m.

Observação: Vale lembrar que o coeficiente angular de uma reta é a medida da tangente do ângulo que a reta forma com o eixo x, no sentido anti-horário.

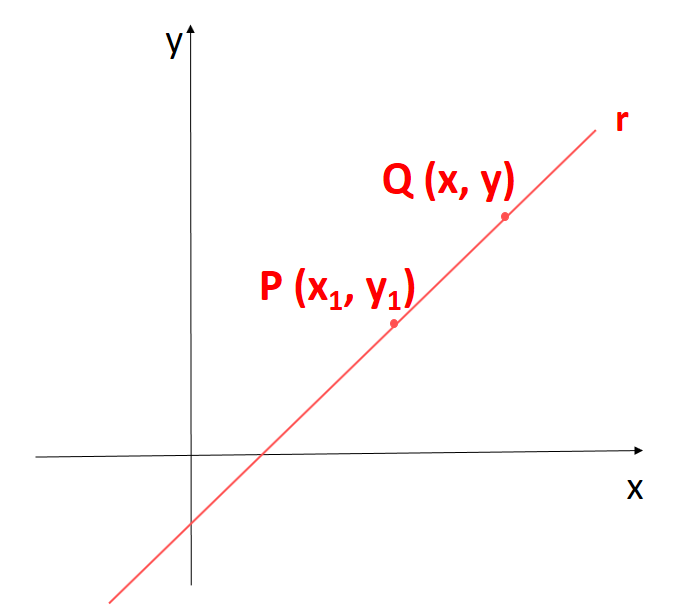
Mantendo o ponto Q (x, y) sobre a reta r, com Q ≠ P, vamos determinar a equação que representa a reta que passa por esses dois pontos.

Utilizando a fórmula do coeficiente angular, temos:

$m=\frac{y-y_1}{x-x_1}\rightarrow y-y_1=m\cdot(x-x_1)$

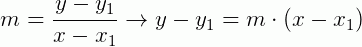
Equação fundamental da reta

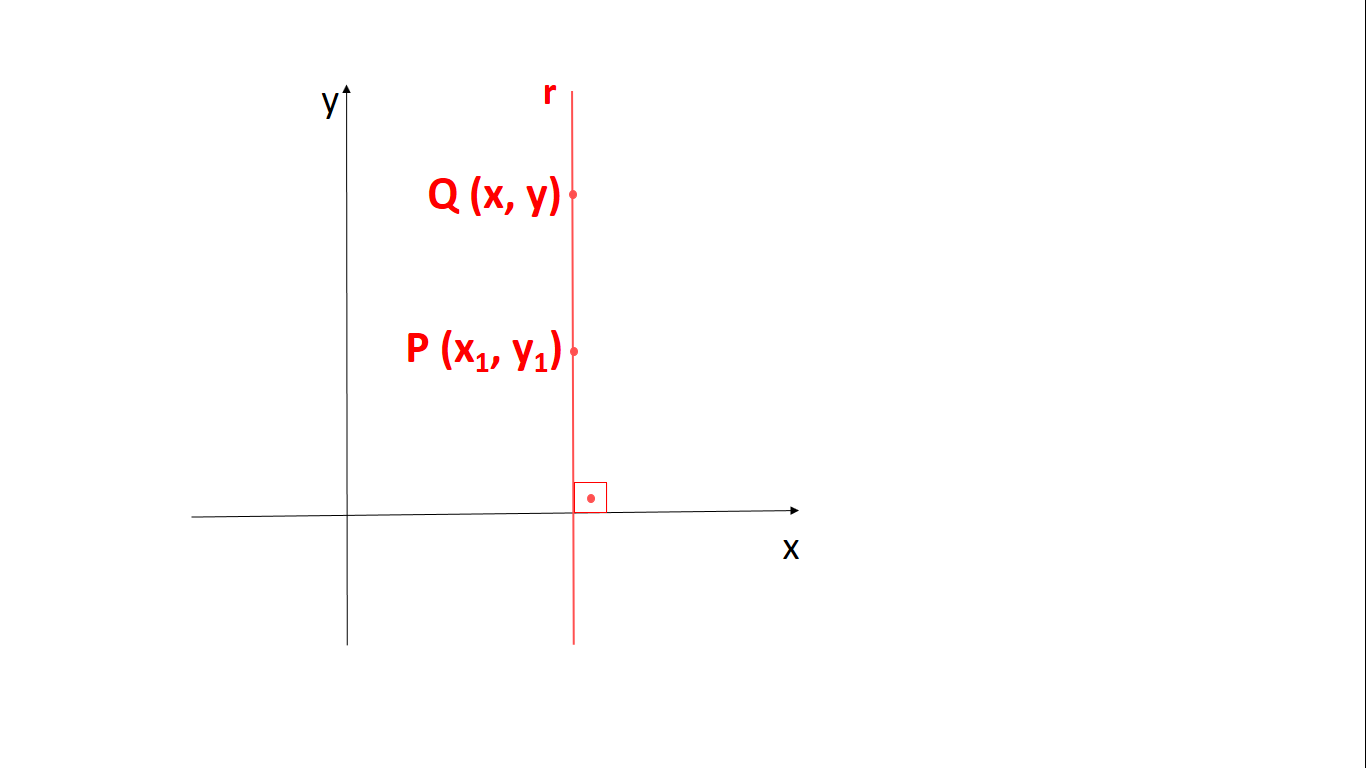
Observação: Se a reta r é vertical, então todos os pontos da reta têm a mesma abscissa. Assim, o ponto Q (x, y) é um ponto qualquer da reta se, e somente se x = x₁.

Exercícios resolvidos

1º) Ache a equação da reta r representada abaixo:

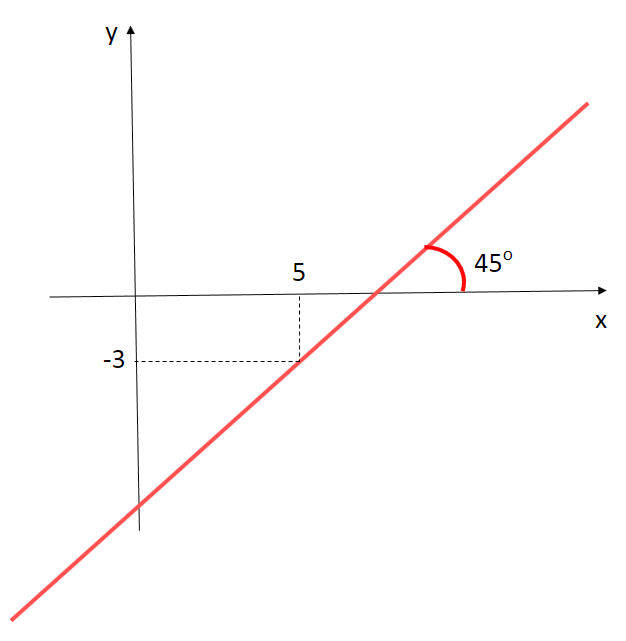
Temos: α = 45^o, x₁ = 5, y₁ = -3 e Q = (x, y)

O coeficiente angular m = tg α = 45^o = 1 e o ponto P = (5, -3)

Substituindo na equação fundamental da reta, temos:

$y-y_1=m\cdot(x-x_1)$

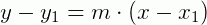
y – (-3) = 1 . ( x – 5) ⇒ y + 3 = x – 5

x – y – 8 = 0

2º) Determine a equação da reta que passa pelos pontos A = (1, 4) e B = (2, 1).

Vamos calcular o coeficiente angular da reta, dados os dois pontos:

$m=\frac{y_B-y_A}{x_B-x_A}=\frac{1-4}{2-1}=\frac{-3}{1}=-3$

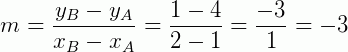
Substituindo na equação fundamental da reta, temos:

$y-y_1=m\cdot(x-x_1)$

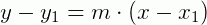
y – 4 = -3 . ( x – 1) ⇒

y - 4 = -3x + 3 ⇒

3x + y - 7 = 0

3º) Dado o ponto A = (-2, 3), calcule as coordenadas do ponto B = (3k, k + 1) de modo que o coeficiente angular da reta AB seja m = ½.

Substituindo na equação fundamental da reta, os valores: x = -2, x₁ = 3k, y = 3, y₁ = k + 1; temos:

$y-y_1=m\cdot(x-x_1)$

$3-(k+1)=\frac{1}{2}(-2-3k)\rightarrow$

$3-k-1=-1-\frac{3k}{2}\rightarrow$

$\frac{3k}{2}-k=-1+1-3\rightarrow$

$\frac{1k}{2}=-3\rightarrow k=-6$

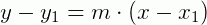
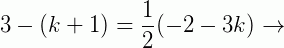
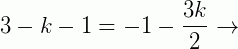
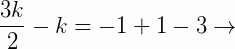
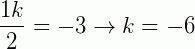
Portanto: B = (-18, -5)

Referências bibliográficas:

1. MURAKAMI, C.; IEZZI, G. Fundamentos de Matemática Elementar: Conjuntos. Funções. Vol. 1. 8ª Ed. Editora: Atual. 2004.

2. LIMA, E. L., et al. A Matemática do Ensino Médio. 9ª ed. Rio de Janeiro: SBM, 2006. v.1

3. DANTE, Luis Roberto. Matemática: contexto e aplicações. Volume único. São Paulo: Editora Ática, 2009.

Texto originalmente publicado em https://www.infoescola.com/matematica/equacao-fundamental-da-reta/