Equação geral da reta

Sempre abrir.

Quando estudamos função, verificamos que uma função do 1º grau é definida por uma expressão algébrica do 1º grau com duas variáveis que o seu gráfico é uma reta.

Reciprocamente, podemos dizer que uma linha reta é representada por uma equação do 1º grau com duas variáveis.

Neste texto, estudaremos a equação geral da reta.

Equação geral da reta

Consideremos a reta r indicada na figura e os pontos A (x₁, y₁) e B(x₂, y₂) sobre ela.

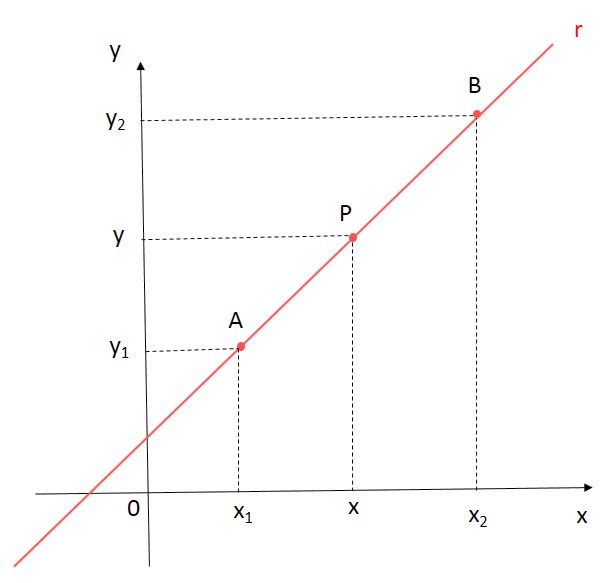
Seja P (x, y) um ponto qualquer dessa reta.

Se os pontos P, A e B são colineares, temos:

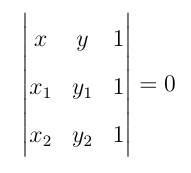
Desenvolvendo o determinante, temos:

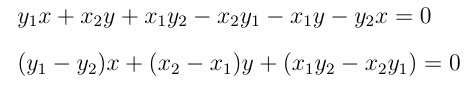
Fazendo

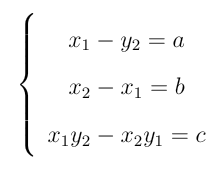
obtemos a equação geral da reta

ax + by + c = 0

com a, b e c constantes.

Assim, podemos afirmar que:

Toda reta possui uma equação da forma ax + by + c = 0, onde a e b não são ambos nulos, que é chamada equação geral da reta.

O coeficiente angular da reta é dado por:

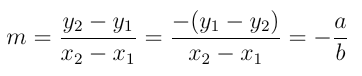
O coeficiente linear da reta é dado por:

$n=-\frac{c}{b}$

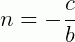
Casos particulares

1º) Se a = 0 e c ≠ 0

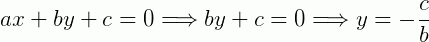
$ax+by+c=0\Longrightarrow by+c=0\Longrightarrow y=-\frac{c}{b}$

Reta paralela ao eixo x

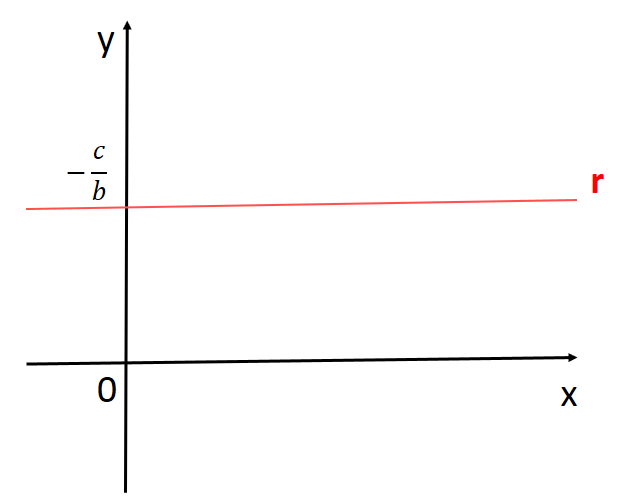
2º) Se b = 0 e c ≠ 0

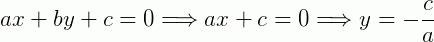
$ax+by+c=0\Longrightarrow ax+c=0\Longrightarrow y=-\frac{c}{a}$

Reta paralela ao eixo y

3º) Se c = 0

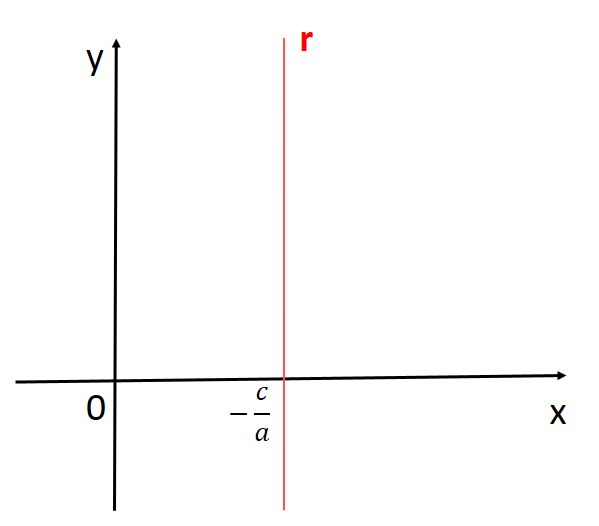
$ax+by+c=0\Longrightarrow ax+by=0$

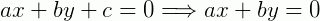
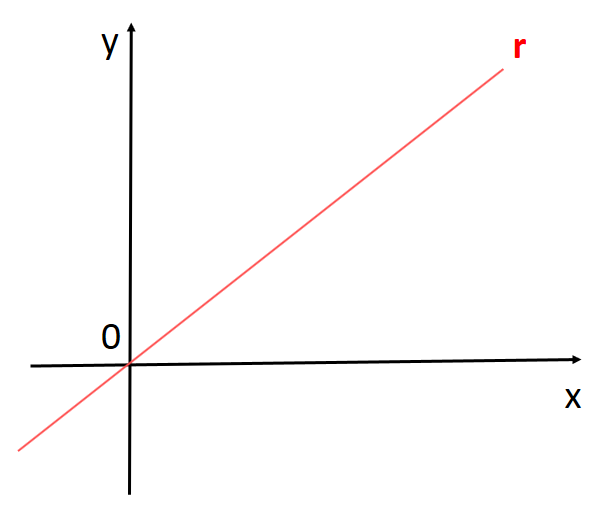
Reta que passa pela origem

Observação: Se tivermos:

x + y = 0 ⇒ reta bissetriz dos quadrantes pares
x – y = 0 ⇒ reta bissetriz dos quadrantes ímpares

Exercícios resolvidos

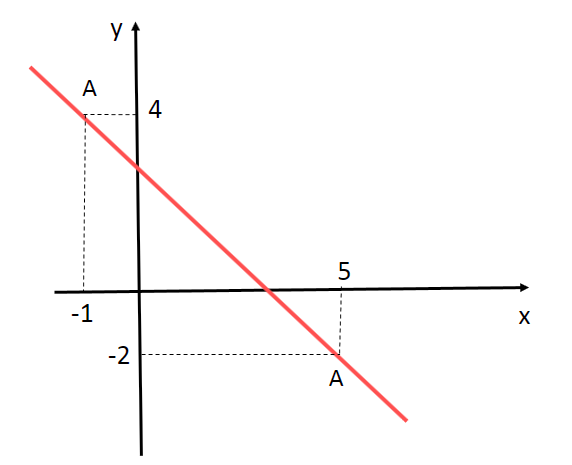
1º) Seja a reta determinada pelos pontos A = (-1, 4) e B = (5, -2). Determine a equação geral dessa reta.

Como os pontos P, A e B devem estar alinhados, e de acordo com a condição de alinhamento de três pontos, temos:

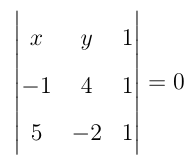
4x + 5y + 2 – 20 + y + 2x = 0

6x + 6y – 18 = 0

x + y – 3 = 0

Resposta: x + y – 3 = 0

2º) Consideremos a reta que passa pelos pontos A = (1, 4) e B = (2, 1). Determine o coeficiente angular e o coeficiente linear dessa reta.

Equação da reta suporte do lado AB.

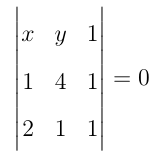
4x + 2y + 1 – 8 - y - x = 0

3x + y – 7 = 0

O coeficiente angular desta reta é dado por:

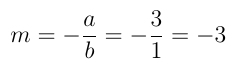
O coeficiente linear desta reta é dado por:

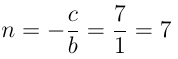
3º) Os pontos A = (1, 2); B = (3, 1) e C = (2, 4) são os vértices de um triângulo. Determinar a equação das retas suportes dos lados desse triângulo.

Equação da reta suporte do lado AB.

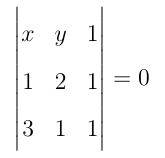
2x + 3y + 1 – 6 - y - x = 0

x + 2y – 5 = 0

Equação da reta suporte do lado AC.

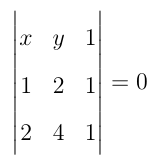
2x + 2y + 4 – 4 - y -4 x = 0

-2x + y = 0

Equação da reta suporte do lado BC.

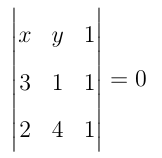
x + 2y + 12 – 2 - 3y - 4x = 0

-3x –y =10 = 0