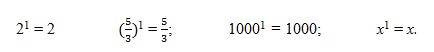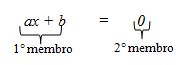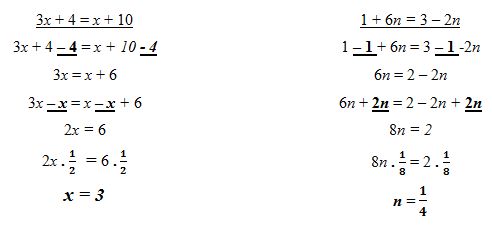Conteúdo deste artigo
Historiando
Milhares de anos atrás, as equações já eram bastante utilizadas. O acesso a essa maravilhosa ferramenta matemática era muito complexo, tendo em vista os poucos recursos matemáticos da época. Os matemáticos hindus usavam conceitos sobre equação para disputarem em concursos públicos de testes intelectuais onde um matemático formulava perguntas para que o outro desse a resposta e vice-versa.
As equações eram também utilizadas para demonstrarem truques de magias, resolução de quebra-cabeças e problemas de diversas naturezas que geralmente eram envoltos num misto de mistério e intelectualidade.
A primeira referência sobre equação que se tem registro data de aproximadamente 4000 anos pretéritos, o Papiro de Rhind. Este documento traz várias inscrições de problemas matemáticos, na maioria, solucionados através de equações. Como os egípcios não detinham o conhecimento algébrico, suas soluções equacionais eram complexas e, praticamente, inacessíveis.
Os matemáticos gregos chegavam à resolução das equações por meios geométricos. Estes, como eram de muito difícil compreensão, ficavam restritos somente às mãos de poucos indivíduos, verdadeiros donos de uma rara inteligência abstrata. Já na Arábia, teve origem uma aproximação do que hoje chamamos de x para indicar valores desconhecidos. Na língua árabe a palavra desconhecida é escrita xay. Numa tradução informal e econômica de letras, nasce o x. O matemático árabe de maior representatividade viveu no século IX, Al- Khowarizmi.
A inserção de símbolos matemáticos e o uso de letras para representarem valores desconhecidos nas equações foram concebidos por Fraçois Viète, matemático francês responsável, também, pelo estudo das propriedades das equações do tipo ax + b = 0, ou seja, equações de 1° grau na incógnita x. Atualmente as equações são conhecidas com o idioma da álgebra.
Incógnitas e coeficientes
Já foi dito que em tempos remotos os valores desconhecidos de um determinado problema eram nomeados pelos árabes de xay e em outros casos, até mesmo por outros povos, a sua referência era feita através de figuras geométricas. Em dias atuais a nomenclatura utilizada para determinar o que se quer encontrar em problemas matemáticos é incógnita. Esta palavra deriva do latim incognitu que também significa coisa desconhecida.
A letra a ser usada para representar o valor desconhecido fica a critério do autor da questão, o que realmente importa é a facilitação do cálculo de equações com a introdução dessa ferramenta algébrica aliada a aritmética, a geometria e tantos outros ramos da matemática. Sendo assim, pode-se, ao invés do x, usar-se a, b, c, d,... z, etc.
Em linguagem matemática, se temos uma expressão do tipo 2x – 4 = 0 destacam-se:
- 2 e 4 são coeficientes – representam respectivamente fator e subtraendo da equação exemplificada;
- x é incógnita – valor desconhecido ao qual se está buscando encontrar;
- para x = 2 temos uma sentença verdadeira, ou seja, 2 . 2 – 4 = 0. Ao valor que substituído pela incógnita torna a sentença verdadeira dá-se o nome de raiz da equação. Nesse caso o algarismo 2 é a raiz da equação 2x – 4 = 0.
Exemplos
- 4x + 16 = 0, 4 e 16 são coeficientes, x é incógnita;
- n – 2 = 0, 1 e -2 são coeficientes (o desprezo do 1 não altera o equilíbrio da equação uma vez 1.n =n) e n é a incógnita;
- 1/3a – 5/3 = 0, 1/3 e 5/3 são coeficientes, a é a incógnita.
A equação de 1° grau
O fundamento das equações é alicerçado no próprio sentido etimológico da palavra equação. Esta palavra deriva de equatione, do latim, e significa equacionar, igualar. Baseado na definição etimológica da palavra equação entende-se que devemos procurar igualar o lado esquerdo ao lado direito da expressão. Quando isso acontece, diz-se que temos uma sentença verdadeira, uma igualdade, uma equação.
Toda expressão do tipo ax + b = 0, com a ≠ 0, representa uma equação de primeiro grau na incógnita x, onde a e b são os coeficientes da equação e x é a incógnita.
O coeficiente a deve ser diferente de zero ou então não teríamos a caracterização de equação, uma vez que o valor da incógnita também assumiria zero, neutralizando a nossa busca pelo elemento desconhecido. Além disso, não seria possível tornar a sentença verdadeira, fundamento primordial da equação. Acompanhem a expressão 0x + 9 = 0:
0x + 9 = 0, como 0 . x = 0 temos
0 + 9 = 0.
A sentença é falsa, pois 9 ≠ 0. Logo não temos uma equação (igualdade).
A caracterização de 1° grau se dá pelo fato da incógnita estar elevada ao expoente 1, vejam:
Por definição, todo número elevado à primeira potência resulta nele próprio. Sendo assim, omite-se o expoente 1, pois sua ausência, nesse tipo de situação, não desequilibra a sentença matemática.
Os princípios da balança, da adição e da multiplicação
Para compreendermos melhor a ideia de igualdade, necessário é que conheçamos o princípio da balança. Este princípio consiste em tornar os dois lados da igualdade equilibrados, com o mesmo “peso”. Basta para isso que imaginemos uma balança de dois pratos em perfeito estado de equilíbrio, ou seja, mesmo peso em ambos os pratos.
Dividamos a equação ax + b = 0 em duas partes. Ao lado esquerdo da igualdade chamaremos primeiro membro e ao lado direito chamaremos segundo membro.
O primeiro membro deverá sempre estar equilibrado em relação ao segundo. Quando adicionamos, subtraímos, multiplicamos ou dividimos um número qualquer no primeiro membro devemos também realizar a mesma operação no segundo membro.
Princípio aditivo
Através do princípio aditivo podemos adicionar ou subtrair os dois membros, simultaneamente, por um mesmo número que teremos uma nova igualdade.
Princípio multiplicativo
Este princípio consiste em multiplicar ou dividir os dois membros, simultaneamente, por um mesmo número. Ao final do processo teremos uma nova igualdade.
Regra prática
Existe um mecanismo prático para solucionar equações. Basta que sigamos algumas dicas:
- Reservaremos o primeiro membro (lado esquerdo da igualdade) somente para os valores desconhecidos (incógnitas);
- Ao segundo membro pertencerão os números não acompanhados da incógnita;
- Quando mudarmos um número ou uma incógnita de um membro para o outro inverteremos seu sinal.
Daniel é filho único e por isso tem uma boa mesada. O seu sonho era comprar uma skate e ser igual aos grandes skatistas brasileiros. Certo dia, ao entrar numa loja, ele encontrou uma ótima promoção: “Compre um skate e leve grátis uma bola de futebol”.
Sabe-se que o triplo do preço do skate com o preço da bola (R$ 50,00) dá um valor de R$ R$ 650,00. Ajude Daniel, encontre o valor unitário do skate.
Chamemos de x o preço skate; 3x é o triplo do preço do skate; R$ 50,00 é preço da bola; R$ 650,00 é a soma de 3x com R$50,00.
Montando a equação
3x + 50 = 650
3x = 650 – 50
3x = 600
x = 600 : 3
x = 200
Portanto, R$ 200,00 é valor unitário do skate. Ainda mais, como foi informado na questão, a bola sairá gratuitamente gerando uma economia de R$ 50,00 caso ela fosse comprada separadamente.
Considerações Finais
Estudar as equações é importante para que sejam facilitadas as resoluções de problemas diários. Com o conhecimento dos conceitos sobre igualdades, podemos desenvolver nosso raciocínio lógico, solucionar problemas contendo valores desconhecidos, operar com os diversos grupos numéricos, passear pelos vários campos da matemática: funções, geometria plana e espacial, logaritmos e todos os ramos da matemática possíveis através do conhecimento das equações.
“Na equação do saber encontraremos uma educação digna e acessível a todos.”
Robison Sá.
Referências bibliográficas
A Origem das Equações do 1º Grau. Disponível em: <http://www.matematiques.com.br/conteudo.php?id=582>. Acesso em: 21 de agosto de 2012.
CENURIÓN, MARÍLIA RAMOS; JAKUBOVIC, JOSÉ; LELIS, MARCELO. Matemática na medida certa: 7ª série, 8°. 7. ed. reform. São Paulo: Scipione, 2007. 256p.
MORI, IRACEMA; ONAGA, DULCE SATIKO. Matemática: desafios e ideias, 6ª série. 14. ed. reform. São Paulo: Saraiva, 2005. 303p.
SOUZA, JOAMIR ROBERTO DE; PATARO, PATRICIA ROSANA MORENO. Vontade de aprender matemática, 8° ano. São Paulo: FTD, 2009. 288p
Texto originalmente publicado em https://www.infoescola.com/matematica/equacoes-de-1-grau-com-uma-incognita/