O desenvolvimento dos logaritmos nasceu da necessidade de simplificação de alguns cálculos matemáticos, principalmente por conta do desenvolvimento da Astronomia e da expansão do comércio causada pelas grandes navegações. Uma maior intensidade nesse desenvolvimento se deu entre os séculos XVI e XVII e os logaritmos surgiram como meios de cálculos, que transformavam complexas operações de multiplicação e divisão em simples operações de adição e subtração.
Conteúdo deste artigo
A invenção do logaritmo
O inventor dos logaritmos foi o escocês John Neper (1550-1617). Mais conhecido por Napier, ele não foi o único de sua época a apresentar desenvolvimentos no campo dos logaritmos, alguns outros matemáticos também apresentaram propostas idênticas à sua.
A proposta de Napier baseou-se numa propriedade já conhecida à época, a multiplicação de potências de mesma base: am . an = am+n, que em linguagem simples quer dizer que a multiplicação de duas potências de mesma base resulta em uma outra potência, formada pela conservação de uma das bases anteriores e elevada ao expoente que resulta da soma dos dois expoentes das potências anteriores.
John Neper
John Neper (Napier) não foi um matemático profissional. Ele era dono de várias propriedades na Escócia, onde administrava os seus bens enquanto escrevia sobre vários assuntos. Prova da versatilidade dele foi à afirmação que ele fez no Livro das Revelações, dizendo que o papa em Roma era o anticristo. Não eram todos os temas da matemática que despertavam o interesse de Napier, especialmente os assuntos ligados à computação e a trigonometria lhes chamava atenção.
Segundo depoimentos do próprio Napier, até que os resultados de suas descobertas sobre os logaritmos fossem publicadas pela primeira vez passaram-se vinte anos, portanto, uma vida dedicada a este assunto. Este fato remete a origem das ideias logarítmicas de Napier ao ano de 1594. Movido por observações das sequências de potências sucessivas, publicadas cinquenta anos antes por Stifel e também nas obras de Arquimedes, ele deparou-se com a evidência de que as somas ou diferenças dos índices das potências eram na verdade produtos ou quocientes das potências dadas, mas com uma particularidade nas sequências de potências inteiras de mesma base, a exemplo do 2, que não poderia ser usada para computações, devido as imprecisões geradas por interpolações realizadas em grandes lacunas entre os termos sucessivos.
O método de Napier
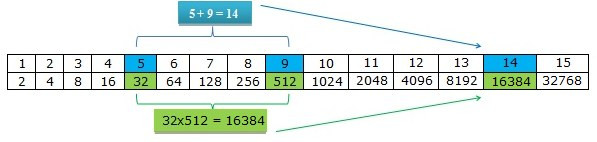
Para melhor compreensão do método de Napier, atente-se na tabela que se segue. Os números da primeira linha são os expoentes, enquanto a segunda linha contém as potências de 2 correspondentes a esses expoentes. Segundo a tabela, podemos calcular produtos complicados, como 32 x 512, operando com uma simples operação de adição.
O que Napier fez foi uma tabela similar a esta, com a ideia de ter facilitado o cálculo de dois números quaisquer. Porém, ele precisaria que a sequência de números da segunda linda fosse formada por números cuja razão se aproximasse de 1, ou seja, ele estava buscando reduzir as lacunas entre os números da segunda linha, o que lhe daria maioria chances de encontrar quaisquer que fosse o produto procurado. Na tabela exemplificada anteriormente a razão é 2, isso gera grandes lacunas entre os números dessa sequência.
Napier solucionou o problema das lacunas utilizando a razão 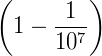 com resultado aproximado a 0,9999999 e para resolver o problema dessas casas decimais que se repetem, ele resolveu multiplicar as potências obtidas com essa razão por 107. A tabela que ele propôs, como reflexo dessas conclusões, foi formada, na primeira linha, pelos expoentes L e na segunda por números N, ficando na forma seguinte:
com resultado aproximado a 0,9999999 e para resolver o problema dessas casas decimais que se repetem, ele resolveu multiplicar as potências obtidas com essa razão por 107. A tabela que ele propôs, como reflexo dessas conclusões, foi formada, na primeira linha, pelos expoentes L e na segunda por números N, ficando na forma seguinte:
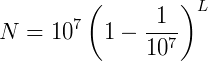
O expoente L foi por ele chamado de logaritmo de N, sendo a palavra logaritmo devida do latim, onde logos = razão e aritmos = número. O Método dos Logaritmos significava para Napier o desejo de expressar a criação de um método de cálculo a partir de razões numéricas ou da proporção de números. Perceba que fazendo L = 0 obteremos N = 107, o que quer dizer que, para Napier, o logaritmo de 107 = 1. Em 1614 John Neper publicou o resultado de suas descobertas no livro Mirifici logarithmorum canonis descriptio (Descrição do maravilhoso método dos logaritmos).
É importante lembrar que Neper principiou a sua obra com explicações que utilizavam termos geométricos. Ele não pensou uma base para o seu sistema, basicamente escrevendo multiplicações repetidas que equivaliam a 0,9999999.
Burgi e Briggs
Na mesma época de Napier, eis que surge, de forma independente, o suíço Joost Burgi (1552-1632) com a proposta de um método idêntico ao dele, empregando uma razão de valor 1,0001, e primeiro termo 108. Burgi criou um método de cálculo de logaritmos e construiu uma tabela com aproximadamente 20 000 termos. Mas foi o matemático inglês Henry Briggs (1561-1630) quem os adaptou para valores mais fáceis de serem utilizados por meio dos logaritmos decimais, como hoje os conhecemos.
“A descoberta acontece na mente dos que se dedicam ao estudo disciplinado.”
(Robison Sá)
Leia também:
- Definição e propriedades dos logaritmos
- Exercícios de Logaritmos
- Aplicações dos Logaritmos
- Mudança de Base de Logaritmos
- Cologaritmo
- Antilogaritmo
Referências bibliográficas:
BOYER, Carl B. História da matemática / Carl B. Boyer, revista por Uta C. Merzbach; tradução Elza F. Gomide – 2ª ed. – São Paulo: Edgard Blucher, 1996.
YOUSSEF, Antonio Nicolau; SOARES, Elizabeth; FERNANDEZ, Vicente Paz. – São Paulo: Scipione, 2005.
Texto originalmente publicado em https://www.infoescola.com/matematica/historia-dos-logaritmos/