Multiplicar frações é uma tarefa extremamente simples. Já sabemos que frações são números representados na forma de uma razão entre de dois números inteiros ou que simbolizam uma proporção. Por exemplo, se dividirmos uma pizza em 8 pessoas, cada uma delas recebeu igualmente  de uma pizza.
de uma pizza.
Para multiplicarmos as frações basta multiplicarmos os denominadores e os numeradores da seguinte maneira:
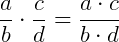
Ou também, se a fração estiver sendo multiplicada por um número a, podemos escrever:
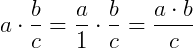
Esta regra vale independente do número de frações que estivermos multiplicando.
Exemplo 1)
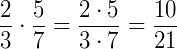
Exemplo 2) Veja abaixo um exemplo de uma multiplicação de um número por uma fração:
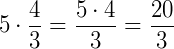
Exemplo 3) Agora com um número maior de frações:
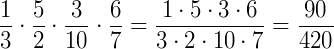
Podemos simplificar o resultado:
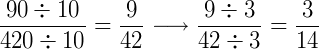
Exemplo 4) Se numa multiplicação de frações alguns denominadores forem iguais aos numeradores, estes podem ser cancelados. Veja:
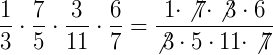
O que nos resulta em:
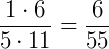
Referências Bibliográficas
DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/multiplicacao-de-fracoes/