Conteúdo deste artigo
Polígonos
Polígonos são figuras geométricas planas que são formadas por segmentos de reta a partir de uma sequência de pontos de um plano, todos distintos e não colineares, onde cada extremidade de qualquer um desses segmentos é comum a apenas um outro.
Eles podem ser côncavos ou convexos. Dados dois pontos A e B, interiores ao polígono, ele será convexo se, e somente se, o segmento de reta AB estiver contido inteiramente no polígono. Caso contrário, ele será côncavo.
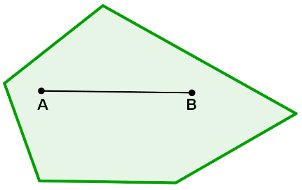
Polígono convexo
A reta AB está inteiramente contida no polígono:
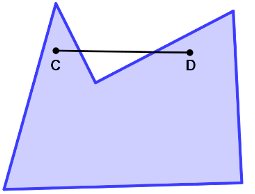
Polígono côncavo ou não convexo
A reta CD não está inteiramente contida no polígono.
Diagonal de um polígono
A diagonal de um polígono é um segmento cujas extremidades são vértices não consecutivos desse polígono:
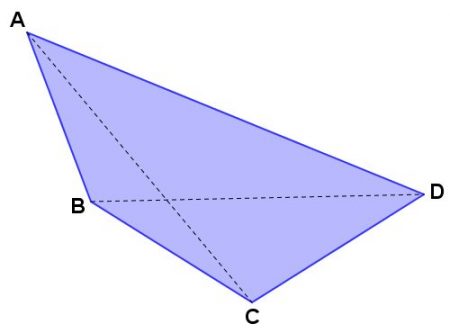
Na figura acima, os segmentos AC e BD são diagonais.
Número de diagonais de um polígono
É possível determinar a quantidade de diagonais que um polígono qualquer de lado n pode ter. Existe uma fórmula matemática que nos dá essa quantidade de diagonais, considerando a quantidade de lados do polígono.
Considere o seguinte polígono, um hexágono regular ABCDEF:
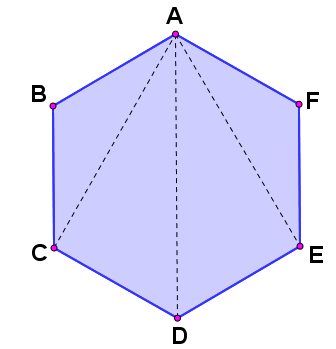
Para cada vértice deste polígono, por exemplo, o vértice A, podemos contar, inicialmente 6 diagonais:
Uma delas é AA (sai de A e vai para ele mesmo), AB, AC, AD, AE, AF.
Mas, pela definição de diagonal, os segmentos AA, AB e AF não são diagonais, pois AA é, em si o próprio vértice A e AB e AF são lados do polígono.
Assim, dos 6 segmentos, apenas 3 são realmente diagonais. Como temos um total de 6 vértices, de cada um deles sairão 3 diagonais, totalizando 6 . 3 = 18 diagonais (observe que estaremos contando, por exemplo, AC e CA como duas diagonais diferentes, por isso sempre devemos dividir esse valor por 2, como veremos, totalizando 9 diagonais para um hexágono).
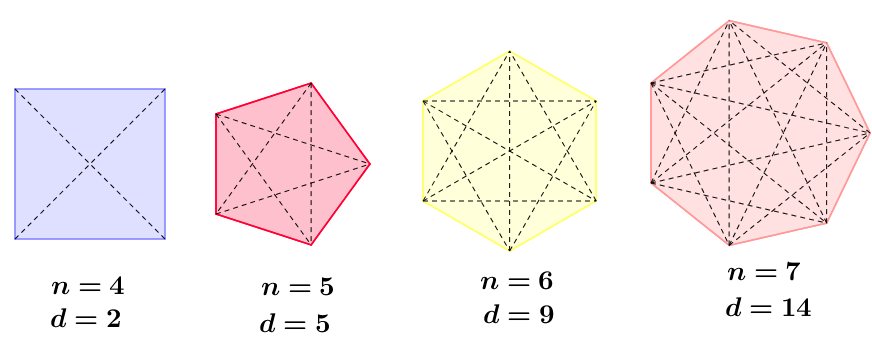
Isso sempre acontecerá em qualquer polígono. Por exemplo, se um polígono tem 8 lados, de cada vértice contamos 8 segmentos, dos quais 3 deles não são considerados diagonais, ou seja, teremos 8 – 3 diagonais, ou seja, apenas 5.
| Número de lados: | 4 | 5 | 6 | 7 | 8 | n |
| Número de diagonais de um vértice: | 1 | 2 | 3 | 4 | 5 | n-3 |
Nesse sentido, para um polígono de n lados, teremos, saindo de cada vértice, n – 3 diagonais. Como temos n vértices, a quantidade de diagonais será n (n - 3).
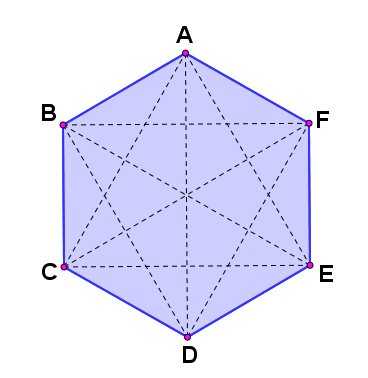
Note que, como dito antes, estamos contando cada diagonal duas vezes. Tomando a figura acima como exemplo, estamos contando que AD e DA são duas diagonais diferentes, quando na verdade é a mesma. Assim, do total de diagonais que calculamos em um polígono, temos que dividir esse valor por 2.
Assim, para um polígono de n lados, teremos uma quantidade de diagonais dada por:
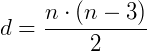
Vale ressaltar que n sempre deve ser maior que 3, pois um polígono de exatamente 3 lados (um triângulo) não possui nenhuma diagonal.
Ilustrando:
Exemplo
Qual a quantidade de diagonais de um polígono de 12 lados?
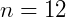
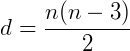
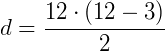
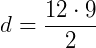
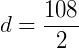
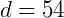
Logo, esse polígono tem 54 diagonais.
Referência:
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.
Texto originalmente publicado em https://www.infoescola.com/matematica/numero-de-diagonais-de-um-poligono/