Números decimais quando dentro de uma raiz quadrada possuem algumas peculiaridades ao calcular o seu valor, mas as propriedades sobre radiciação continuam valendo. Seja a igualdade 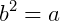 dizemos que b é a raiz quadrada de a, ou seja:
dizemos que b é a raiz quadrada de a, ou seja:
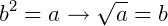
O símbolo 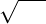 é conhecido por radical, a é o radicando e n é o índice.
é conhecido por radical, a é o radicando e n é o índice.
Propriedades de radiciação
1. 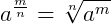
2. 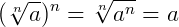
3. 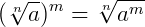
4. 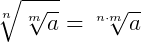
5. 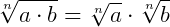
6. 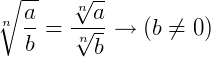
7. 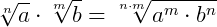
8. 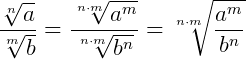
9. 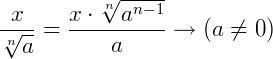
10. 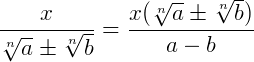
Como estamos lidando apenas com raízes quadradas de números decimais neste texto, consideremos a partir de agora que o índice sempre será 2.
Calculando o valor de raízes
Exemplo 1) Vamos calcular o valor de 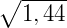 .
.
O método mais simples para calcularmos essa raiz é aquele em que transformamos o número decimal em uma fração:
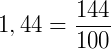
Então, se seguirmos a propriedade (6), temos:
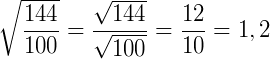
Exemplo 2) Calcule 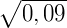 .
.
Transformando em fração: 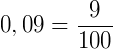 .
.
Então: 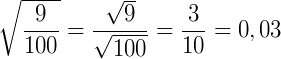 .
.
Exemplo 3) Agora, vamos calcular um número decimal com dízima periódica numa raiz quadrada:
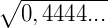 ou
ou 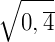
Ao calcularmos a fração geratriz de 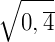 obtemos:
obtemos:
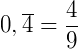
Então:
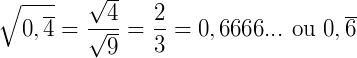
Exemplo 4) Um exemplo interessante agora. Vamos calcular:
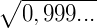 ou
ou 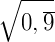
Ao calcularmos a fração geratriz de obtemos:
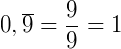
Então:
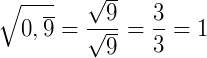
Esta é uma das formas de provar que 0,999... = 1.
Referências Bibliográficas
DEMANDA, Franklin D; WAITS, Bert K.; FOLEY, Gregory D.; KENNEDY, Daniel. Pré Calculo. São Paulo: Pearson, 2013.
MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.
Texto originalmente publicado em https://www.infoescola.com/matematica/raiz-quadrada-de-numeros-decimais/