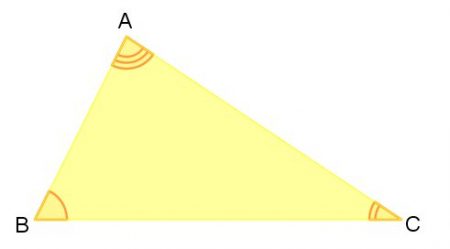
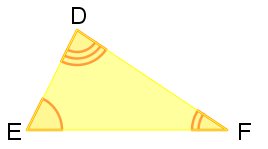
Dois triângulos são semelhantes se, e somente se, seus três ângulos são congruentes (na mesma ordem) e seus lados homólogos são proporcionais.
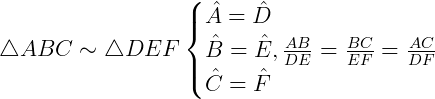
O símbolo 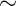 significa “semelhante”.
significa “semelhante”.
Cada um dos lados homólogos está em um triângulo e ambos são opostos a ângulos congruentes.
Conteúdo deste artigo
Razão de semelhança
A razão entre dois lados homólogos ou entre dois triângulos semelhantes (k) é chamada de razão de semelhança.
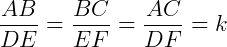
Exemplo:
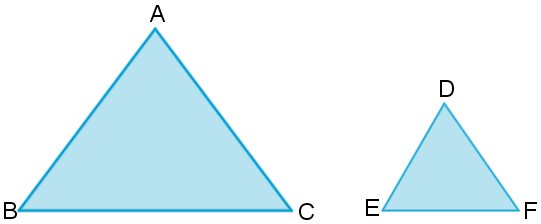
Por exemplo, os triângulos abaixo são semelhantes:
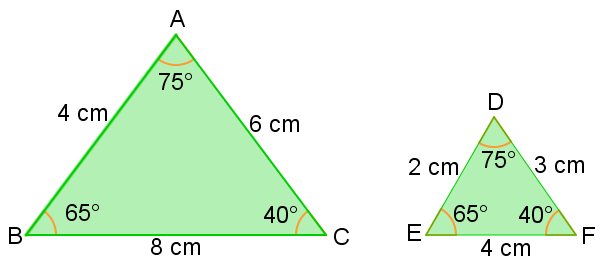
Os ângulos são congruentes (iguais) e os lados homólogos são proporcionais.
Note que 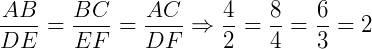 .
.
A razão de semelhança será k = 2. Podemos dizer que o triângulo ABC é 2 vezes maior que DEF ou que DEF é duas vezes menor que ABC.
Propriedades
Da definição de triângulos semelhantes decorrem as seguintes propriedades:
1. reflexiva: um triângulo é semelhante a ele mesmo.
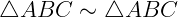
2. simétrica: se 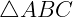 o é semelhante ao
o é semelhante ao 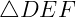 , então o
, então o 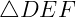 é semelhante ao
é semelhante ao 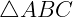 .
.
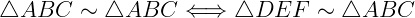
3. transitiva: se o 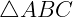 é semelhante ao
é semelhante ao 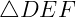 , e
, e 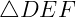 é semelhante a outro
é semelhante a outro 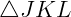 , então o
, então o 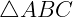 é semelhante ao
é semelhante ao 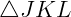 .
.
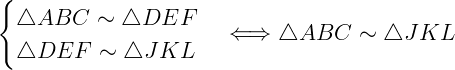
Teorema fundamental
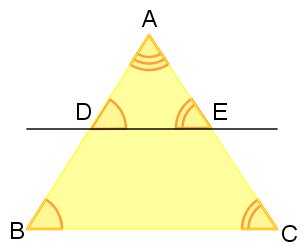
Se houver uma reta paralela a um dos lados de um triângulo e ela intercepta os outros dois lados em pontos distintos, dois triângulos serão formados e eles serão semelhantes.
Casos de semelhança
Para se verificar que dois triângulos são semelhantes, não é necessário conferir se todos os lados homólogos são proporcionais e que todos os ângulos são congruentes. Há alguns casos em que a detecção da semelhança é facilitada.
Caso AA (Ângulo, Ângulo)
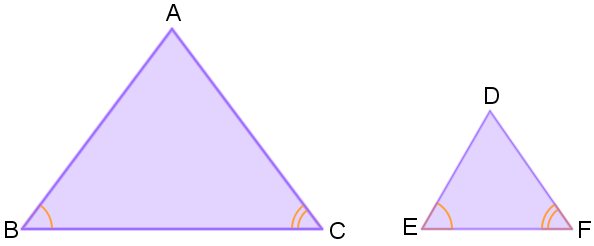
Sejam dois triângulos ABC e DEF. Eles serão semelhantes se, e somente se, dois de seus ângulos forem congruentes.
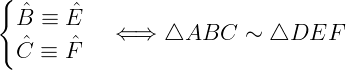
Caso LAL (Lado, Ângulo, Lado)
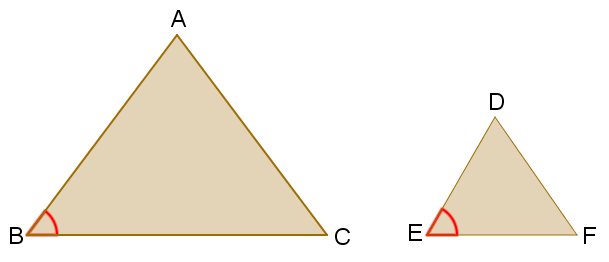
Dois triângulos serão semelhantes se, e somente se, eles tiverem dois lados respectivamente proporcionais e se os ângulos formados por esses lados forem congruentes.
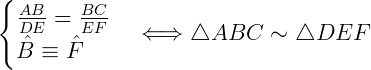
Caso LLL (Lado, Lado, Lado)
Dois triângulos serão semelhantes se, e somente se, eles tiverem os três lados respectivamente proporcionais.

Razão entre áreas
A razão entre as áreas de dois triângulos semelhantes é dada pelo quadrado da razão de semelhança entre eles.
Observe a pequena demonstração:
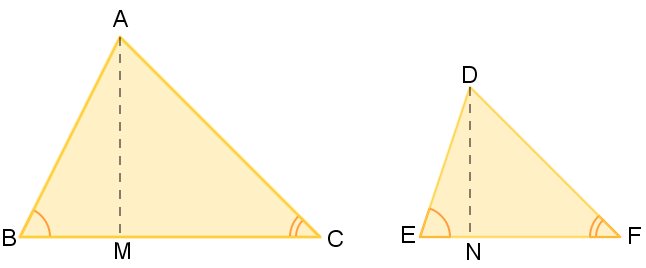
A área do triângulo ABC será: 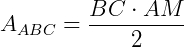 .
.
A área do triângulo DEF será: 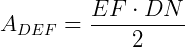 .
.
Dividindo a área do primeiro pela do segundo temos:
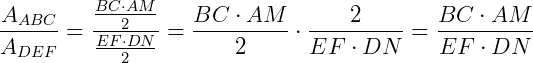
Mas, como os triângulos são semelhantes, temos que 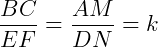 .
.
Assim:
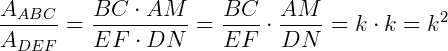
Portanto, teremos que:
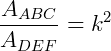
Congruência de triângulos
Dois triângulos são congruentes de a razão de semelhança for k = 1. Esses triângulos possuem os ângulos e os lados homólogos ambos congruentes.


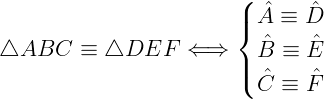 e
e 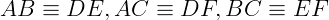 .
.
Exemplo:
1. As figuras abaixo nos mostram pares de triângulos semelhantes, dessa forma calcule os valores de e x e y:
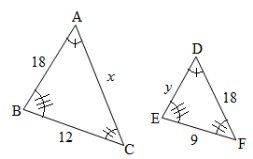
Observando os lados e os ângulos, os lados homólogos são: AB e DE, AC e DF, BC e EF. Assim, para encontrar y fazemos:
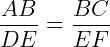
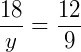
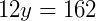
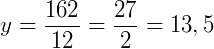
Para encontrar x fazemos:
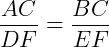
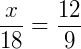
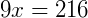
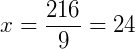
Referências bibliográficas:
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.
RIBEIRO, Paulo Vinícius. Matemática: Semelhança de triângulos. Vol. 2. São Paulo: Bernoulli.
Texto originalmente publicado em https://www.infoescola.com/matematica/semelhanca-de-triangulos/