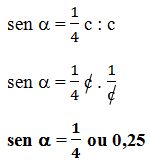Há muito tempo, medições eram realizadas de formas indiretas, principalmente referentes aos corpos celestes, vista a sua importância para a navegação, bem como para “prever o futuro” – para os crédulos. Com o estudo das relações métricas no triângulo retângulo, estas medidas se tornaram mais eficientes, mais precisas. Este será o tema deste artigo, sendo o seu debate possibilitador de novas visões matemáticas e explicitador de ferramentas matemáticas capazes de tornar viáveis os cálculos outrora impossíveis.
Conteúdo deste artigo
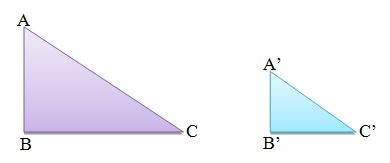
A semelhança de triângulos
Dados dois triângulos, por exemplo, eles serão semelhantes se obedecerem a alguns padrões. Vejam um caso de semelhança e suas relações.
- Em triângulos semelhantes o quociente entre os pares de lados correspondentes forma sempre uma razão constante.
- A razão entre o cateto menor e o cateto maior, nos dois triângulos, é igual.
- A razão entre o cateto maior e a hipotenusa é igual nos dois triângulos.
- A razão entre o cateto menor e a hipotenusa é igual nos dois triângulos.
Razões trigonométricas
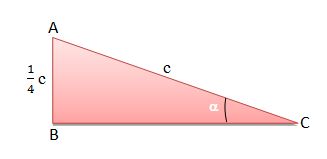
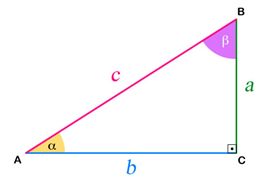 Ao compararmos duas grandezas por meio de uma divisão estaremos dando sentido ao conceito de razão. A palavra razão é etimologicamente ligada ao termo ratio, que traduzido do latim significa, entre outras coisas, rateio, repartição.
Ao compararmos duas grandezas por meio de uma divisão estaremos dando sentido ao conceito de razão. A palavra razão é etimologicamente ligada ao termo ratio, que traduzido do latim significa, entre outras coisas, rateio, repartição.
Observação: as relações são dadas tomando como referência o ângulo α, destacado em amarelo.
A partir destas informações, caso tenhamos alguns ângulos e os valores dos catetos oposto e adjacente, e também da hipotenusa, poderemos encontrar os valores do seno, do cosseno e da tangente desses ângulos. Em seguida mostrarei uma tabela, para consulta, contendo alguns valores de ângulos, seno e cosseno deles, deixando o valor da tangente como exercício para você, estudante.
|
Ângulo |
Seno |
Cosseno |
|---|---|---|
|
5º |
0,09 |
0,99 |
|
15º |
0,26 |
0,97 |
|
30º |
0,50 |
0,87 |
|
45º |
0,71 |
0,71 |
|
65º |
0,91 |
0,42 |
|
75º |
0,97 |
0,26 |
|
85 |
0,99 |
0,09 |
Aplicação dos conceitos
Num triângulo retângulo, o cateto oposto a um ângulo é a quarta parte da hipotenusa. Calcule o seno e dê a medida aproximada desse ângulo, consultando a tabela acima.
- chamemos a hipotenusa de c;
- o cateto oposto, segundo o enunciado, será ¼ c;
- vamos chamar o ângulo de α.
Veja como fica o problema em sua representação abaixo:
Sendo ![]() , podemos prosseguir da seguinte maneira:
, podemos prosseguir da seguinte maneira:
Pela tabela anterior, sabemos que este valor é uma aproximação do seno do ângulo de 15º.
“Seja por qual for o caminho, sempre chegaremos a algum lugar”.
(Robison Sá)
Referência bibliográfica:
IMENES, LUIZ MÁRCIO; LELLIS, MARCELO. Matemática. – 2 ed. –São Paulo: Moderna, 2012.
Texto originalmente publicado em https://www.infoescola.com/matematica/trigonometria-do-triangulo-retangulo/