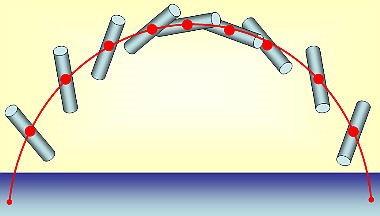
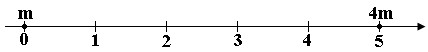Veja a figura a cima. Enquanto o cilindro, lançado para cima, gira, há um ponto seu que não gira, mas descreve uma trajetória parabólica. É o centro de massa do cilindro.
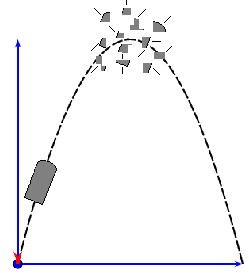
Na figura anterior, o projétil descreve uma trajetória parabólica até explodir. Depois da explosão, cada fragmento tem trajetória diferente, mas o centro de massa do projétil de antes da explosão mantém a trajetória parabólica.
O movimento de um corpo rígido, ou de um sistema de corpos rígidos, pode ser representado pelo movimento do centro de massa desse corpo ou sistema. Pra isso, admite-se que toda a massa do corpo, ou do sistema, esteja concentrada no centro de massa e que nele estejam aplicadas todas as forças externas.
Conteúdo deste artigo
Centro de massa
Considere um sistema de pontos materiais P1, P2,..., Pn e de massas m1, m2,..., mn, respectivamente. Vamos supor, por exemplo, que estes pontos pertençam a um plano α. Admitamos, ainda, conhecidas as coordenadas de P1, P2,..., Pn em relação a um sistema cartesiano ortogonal pertencente ao plano α (Figura): P1 (x1, y1), P2 (x2, y2),..., Pn (xn, yn).
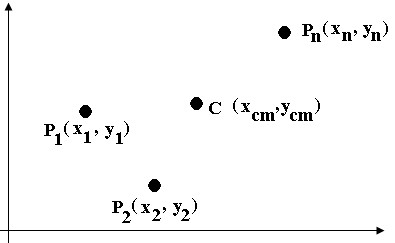 O ponto C de coordenadas (xCM, yCM) obtidas através das médias ponderadas:
O ponto C de coordenadas (xCM, yCM) obtidas através das médias ponderadas:
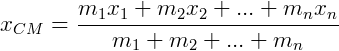
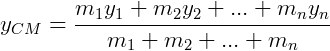
Recebe o nome de centro de massa do sistema de pontos materiais.
Propriedades do centro de massa
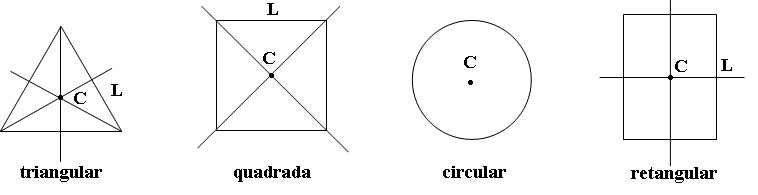
Se o sistema de pontos materiais admite um eixo (ou um centro de simetria), de modo que as massas dos pontos simétricos sejam iguais, então o centro de massa pertence ao eixo (ou ao centro) de simetria.
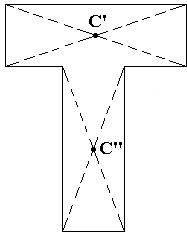
Considere uma chapa homogênea, como por exemplo, a chapa homogênea em forma de T da Figura. Seu centro de massa C coincide com o centro de massa dos pontos C’ e C” que são os centros de massa das chapas retangulares indicadas na figura. Pode-se generalizar a propriedade anterior, subdividindo-se o sistema em mais de dois conjuntos parciais.
 Exercícios Resolvidos
Exercícios Resolvidos
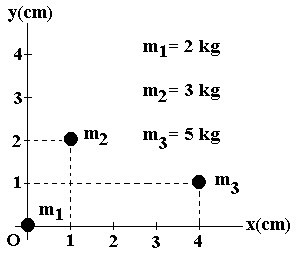
01. Determine as coordenadas do centro de massa do sistema de partículas indicado ao lado.
As coordenadas das partículas são:
m1 → x1 = 0 ; y1 = 0
m2 → x2 = 1; y2 = 2
m3 → x3 = 4 ; y3 = 1
Deste modo, as coordenadas do centro de massa são:
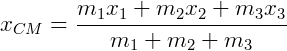
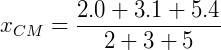
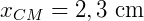
.
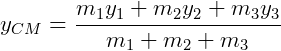
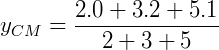
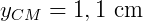
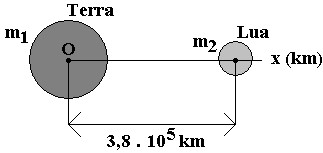
02. A distância entre o centro da Terra e o centro da Lua mede 3,8 . 105 km. A massa da Terra é 82 vezes maior que a massa da Lua. A que distância do centro da terra encontra-se o centro de massa do sistema Terra-Lua.
Resolução:
Vamos adotar um eixo Ox passando pelos centros da Terra e da Lua, com origem no centro da Terra. Nestas condições, a abscissa do centro de massa da Terra é nula (x1 = 0) e da Lua é x2 = 3,8 . 105 km. Sendo m2 a massa da Lua e m1 = 82m2 a massa da Terra, vem:
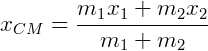
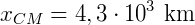
Exercícios Propostos
01. Determine a abscissa do centro de massa do sistema de partículas ao lado, cujas massas são m e 4m.
Resposta: 4 cm.
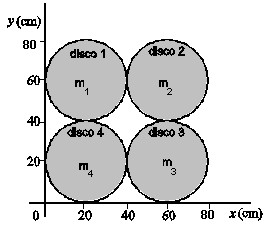 02. Quatro discos, 1, 2, 3 e 4, todos de mesmo raio R = 20 cm, e de massas m1 = 1 kg, m2 = 2 kg, m3 = 3 kg, e m4 = 4 kg estão arrumados no plano horizontal, xy, conforme mostra a figura abaixo. A distribuição de massa em cada disco é homogênea. As coordenadas (X, Y) do centro de massa desse conjunto de discos são dadas, em cm, pelo par ordenado:
02. Quatro discos, 1, 2, 3 e 4, todos de mesmo raio R = 20 cm, e de massas m1 = 1 kg, m2 = 2 kg, m3 = 3 kg, e m4 = 4 kg estão arrumados no plano horizontal, xy, conforme mostra a figura abaixo. A distribuição de massa em cada disco é homogênea. As coordenadas (X, Y) do centro de massa desse conjunto de discos são dadas, em cm, pelo par ordenado:
A) (40, 40)
B) (20, 32)
C) (20, 60)
D) (40, 32)
E) (40, 20)
Resposta: (X,Y) = (40,32), opção D
Texto originalmente publicado em https://www.infoescola.com/mecanica/centro-de-massa/