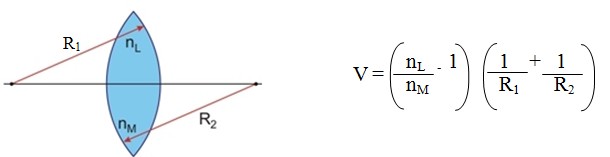A velocidade da luz no vácuo é de aproximadamente 300.000 Km/s. Já em outros materiais transparentes ou translúcidos essa velocidade é menor. A área de contato entre dois materiais diferentes é chamada Dioptro. Ao atravessar um dioptro a luz perde velocidade sofrendo uma inclinação que depende dos materiais que a luz atravessa.
Essa perda de velocidade é conhecida a partir do índice de refração de cada substância. Exemplos de dioptro são o a superfície de contato do vidro com o ar, da água com o ar ou do vidro com a água.
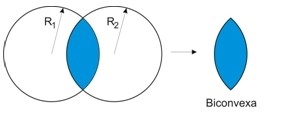
Se a superfície for curva como o arco de um círculo, podemos desviar ou concentrar os raios de luz em um único ponto. O resultado é que as imagens vistas através deste aparelho serão maiores, menores, invertidas ou não. Assim formam-se as lentes.
Uma lente possui dois dioptros, um de cada lado. O raio do círculo que serviu como base para a superfície da lente é chamado de Raio de Curvatura. Como convenção, a face convexa possui raio positivo, a face côncava possui raio negativo e a face plana possui raio infinito.
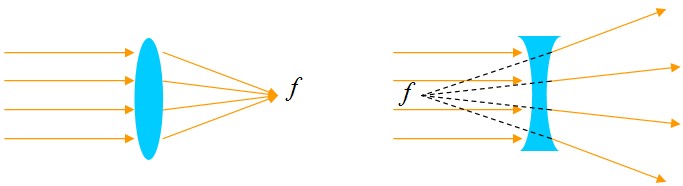
Quando uma lente é atravessada por um feixe de raios paralelos, esses raios se concentram em um único ponto, esse ponto é chamado foco.
Quanto menor o foco, maior a capacidade da lente de desviar os feixes de luz. A isso chamamos Vergência, definida por:
V = 1/f
Onde V é a Vergência e fé a distância do vértice da lente até o foco.A Unidade de medida S.I. da Vergência é a dioptria (di) e a do foco é o metro (m).
Uma equação que envolve todos essas variáveis é a Equação dos Fabricantes de Lentes. Ela possui esse nome porque envolve valores facilmente encontrados para uma lente comum, permitindo calcular a Vergência conhecendo os raios da lente ou vice-versa.
Observe a lente a seguir:
Onde:
R1 - raio de curvatura da superfície 1;
R2 - raio de curvatura da superfície 2;
nL- índice de refração do material que constitui a lente;
nM- índice de refração do meio em que a lente se encontra.
Exemplo:
Considere, uma lente biconvexa com raios de curvatura iguais a 20 cm cada uma. O índice de refração relativo é 1,5. Determine a distância focal e a vergência da lente. (Considere o índice de refração do ar igual a 1)
Usando a equação dos Fabricantes de Lentes :
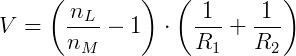
Substituindo os valores:
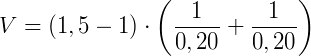
Obtemos:
V = 5 di
Como f = 1/v, temos:
f = 1 / 5
f = 0,2 m
Fontes:
https://web.archive.org/web/20140524085640/http://educar.sc.usp.br:80/otica/lente.htm
http://efisica.if.usp.br/otica/basico/lentes/equacao/
Texto originalmente publicado em https://www.infoescola.com/optica/equacao-do-fabricante-de-lentes/