Uma matriz invertível (ou não singular) é uma matriz, necessariamente quadrada, que admite uma inversa. Para melhor compreensão deste tema, é importante visitar os artigos sobre determinantes de matrizes e multiplicação de matrizes. Sendo assim, dada uma matriz A e supondo que ela seja invertível, então existe uma única matriz B tal que:
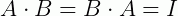
Onde I é a matriz identidade e B é a matriz inversa de A. Podemos também representar a matriz inversa de A com a notação A-1, ao invés de usar B, ou seja:
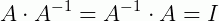
É importante definir que, para uma matriz ser invertível é necessário que o seu determinante seja diferente de zero:
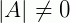
Inversa de matrizes de ordem 2
Começando com um caso geral de inversão de matrizes de ordem 2, podemos afirmar que dada uma matriz A onde a, b, c e d são valores constantes:
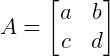
O que devemos fazer é encontrar uma matriz inversa de A e, para isso iremos supor que exista A-1 tal que:
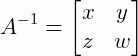
Então, pela relação:
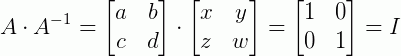
Multiplicando estas matrizes obtemos:
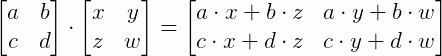
E consequentemente:
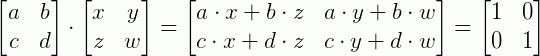
Perceba que agora chegamos a uma igualdade entre duas matrizes, o que nos possibilita escrever cada elemento de 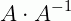 com o seu correspondente em I. Logo:
com o seu correspondente em I. Logo:
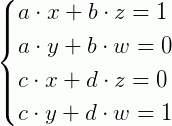
O que reduz nosso problema para um sistema linear de equações que pode também ser dividido em dois sistemas em termos das variáveis:
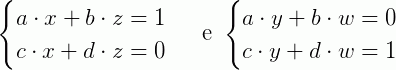
Este é um caso geral. Agora vamos a um exemplo prático. Suponha uma matriz:
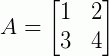
Para determinar a sua inversa, devemos:
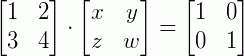
Ou seja:
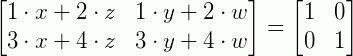
Separando em dois sistemas e resolvendo-os (visite os artigos Sistemas de Equações e Resolução de Sistemas Lineares para recordar os métodos de solução de sistemas), temos:
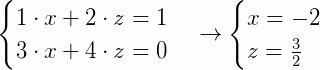
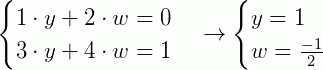
Então, a matriz inversa de A é:
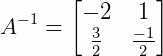
Inversa de matrizes de ordem n
Suponha que A seja uma matriz de qualquer ordem n. Encontrar a matriz A-1 se resume a encontrar a solução de um sistema de n equações com n incógnitas. De modo geral, suponha:
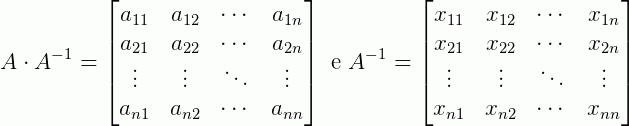
Então,

Referências bibliográficas:
ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed. Rio de Janeiro: Elsevier, 2017.
LIPSCHUTZ, Seymor; LIPSON, Marc. Álgebra Linear – 4ª Ed. Porto Alegre: Bookman, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/matriz-inversa/