A primeira lei de Newton (ou lei da inércia) diz que um corpo só modifica seu estado se uma força for aplicada sobre ele. No entanto, mais de uma força podem agir sobre um corpo ao mesmo tempo. Aliás, é o mais comum de acontecer. Sendo assim, Newton estabeleceu uma lei que representa o efeito de todas as forças que agem sobre um corpo e que resultam em movimento.
A Segunda Lei de Newton (princípio fundamental da dinâmica) afirma que:
“A resultante das forças que agem sobre um corpo de massa constante se dá pelo produto dessa mesma massa pela aceleração resultante.”
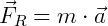
Ou seja, o que vai fazer um corpo modificar seu estado original (seja iniciar um movimento, mudar sua trajetória ou parar) será a resultante de todas as forças que agem sobre este.
A equação acima nos fornece a resultante dessas forças e é chamada de equação fundamental da dinâmica.
Imagine uma brincadeira de cabo de guerra – cada equipe puxa a extremidade de uma corda para si. No meio da corda tem um nó e ganha a equipe que conseguir fazer esse nó passar para o seu lado no campo. Se as duas equipes puxam a corda com a mesma intensidade (força) elas se anulam e a corda não se move. No entanto, se uma equipe puxa a corda com um pouco mais de força, vai conseguir fazer a corda se mover em sua direção e ganhará o jogo. Repare que ambas as equipes aplicaram força na corda, mas aquela que teve maior força gerou uma força resultante em sua direção. Assim, perceba que a aceleração vai ter direção e sentido coincidentes à força resultante, pois é esta (a força resultante) que vai dar aceleração ao corpo.
De acordo com suas causas, eis dois exemplos de forças:
Força Peso (P): força de atração que a Terra (por meio da aceleração da gravidade - g) exerce sobre um corpo.
Estamos todos (pessoas, animais, objetos e afins) presos a Terra, pois a todo o momento somos atraídos para o seu centro. Assim, sempre que lançamos uma bola para o alto, por exemplo, ela retornará a Terra.
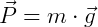
Força Elástica (F): força gerada devido à deformação de uma mola. Se uma mola é comprimida ou distendida, sua tendência é voltar ao seu estado normal.
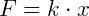
No caso da força elástica, para facilitar, seu valor é dado por uma fórmula (Lei de Hooke) que leva em conta as características da mola e não da massa que está presa a ela. Na equação acima, k é a constante elástica da mola (unidade: N/m), que caracteriza sua capacidade de voltar ao estado normal quando deformada; e x é a deformação (em metros – m) que a mola sofre.
Leia também:
Texto originalmente publicado em https://www.infoescola.com/fisica/segunda-lei-de-newton-principio-fundamental-da-dinamica/