Aceleração angular

Um objeto realiza uma trajetória circular com velocidade angular (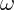$\omega$) variável ao longo do tempo. Assim, da mesma forma que há a aceleração escalar para caracterizar como velocidade escalar varia ao longo de tempo, temos também a aceleração angular.

Então, um objeto que sofre uma variação da velocidade angular 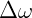$\Delta\omega$ em um determinado intervalo de tempo 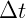$\Delta t$ tem a seguinte aceleração angular média $\gamma_m$:

$\gamma_m = \frac{\omega_f - \omega_i}{t-t_0}$

$\gamma_m = \frac{\Delta\omega}{\Delta t}$

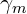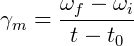
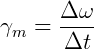
Quanto mais aproximamos os valores do tempo final e inicial do intervalo de tempo da trajetória, mais próximos ficamos de 0, ou seja, do valor a aceleração instantânea (γ):

$\gamma = \underset{\Delta t \to 0}{\lim} \frac{\Delta\omega}{\Delta t}$

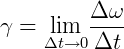
(lê-se limite de Δt tendendo a zero)

Lembrando que, uma vez que a velocidade angular é dada em rad/s, a aceleração angular será dada em rad/s².

Da relação entre espaço linear e angular, mencionada no início do texto, temos:

$\theta = \frac{S}{R}$

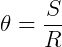
Que resulta em:

$v = \omega R$

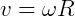
Ou

$\omega = \frac{v}{R}$

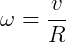
Para a aceleração, temos:

$\Delta v = \Delta\omega R$

$\frac{\Delta v}{\Delta t} = \frac{\Delta\omega R}{\Delta t}$

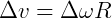
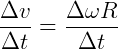
Então:

$\alpha = \gamma R$

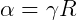
Ou

$\gamma = \frac{a}{R}$

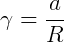
Referências:

Os Fundamentos da Física – Moderna Plus. Ramalho, Nicolau e Toledo. Vol. 01. Moderna. 11ª Ed. SP. 2016

Texto originalmente publicado em https://www.infoescola.com/fisica/aceleracao-angular/