Compton consegue explicar a natureza corpuscular da radiação experimentalmente em 1923. Ele projetou um mecanismo que fizesse com que um feixe de raios X de comprimento de onda λ incidisse sobre um alvo de grafite. Ele observa que há uma relação entre desvio do elétron e o desvio sofrido pelo fóton emergente, que será discutida a seguir, em uma análise particular da interação entre um fóton e um elétron.
Considere um fóton em rota de colisão com um elétron, conforme mostra a figura 01:

Figura 01: representação dos instantes anterior e posterior à colisão entre fóton e elétron
Quando um fóton incide em um elétron, há uma transferência de momento linear e de energia cinética. A energia de um fóton é dada por:
E = h.f (1.a)
Chamaremos E0 a energia do fóton incidente, de modo que nos limitaremos a escrever:
E0 = h.f (1.b)
Sabemos que a energia relativística total de uma partícula que se move com velocidades relativísticas é dada pela expressão:
E² = c².pe² + m0².c4 (2.a)
De forma que podemos escrevê-la para o elétron:
E² = c².pe² + m0².c4 (2.b)
Para o fóton incidente esta energia é dada por
E0² = c².p0² + m0².c4 (2.c)
O termo que contém a massa de repouso é zero, pois o fóton não possui massa de repouso. Desta forma, para o momento linear p0 do fóton incidente, obtemos:
p0 = E0/c (3.a)
Que pode ser escrito em função do produto da constante de Planck pela sua frequência, h.f, o que dá:
p0 = h/λ0 (3.b)
O momento linear p’ do fóton emergente é dado por
p’ = E’/c (3.c)
Que pode ser escrito como:
p' = h/λ’ (3.d)
O momento linear do elétron emergente pe é dado por:
pe = me.ve (4.a)
O momento linear se conserva, logo para a forma vetorial do momento linear total obteremos:
p0 = p’ + pe (5.a)
O qual pode ser decomposto nas componentes ao longo dos eixos x e y, e então escrito em função dos ângulos de espalhamentos em relação à linha da trajetória inicial, na direção x:
p0 = p’.cosθ + pe.cosφ (6.a)
E, na direção y, teremos:
p'. senθ = pe.senφ (7.a)
Elevando ao quadrado as respectivas equações, obtemos:
(p0 – p’.cosθ)² = pe².cos²φ
O que dá, para a componente x:
p0² – 2p0.p’.cosθ + p’².cos²θ = pe².cos²φ (6.b)
E, para a componente y:
p'².sen²θ = pe².sen²φ (7.b)
Fazendo a soma das duas últimas equações, obtemos:
p'².sen²θ + p0² – 2. p0.p’.cosθ + p’².cos²θ = pe².(sen²φ + cos²φ) (8.a)
Sabe-se que
sen²φ + cos²φ = 1 (9)
Desta forma obtemos:
p0² + p’².(sen²θ + cos²θ) – 2. p0.p’.cosθ = pe² (15)
Sabe-se que
sen²θ + cos²θ = 1 (10)
Então, obtemos:
p0² – 2. p0.p’.cosθ + p’² = pe² (11.a)
A energia relativística total é conservada. Logo, podemos escrever:
E0 + m0.c² = E’ + K + m0.c² (12.a)
Os termos m0.c² se anulam, e obtemos:
E0 – E’ = K (13.a)
Podemos escrever esta expressão usando os resultados das equações (3.a) e (3.b)
c.(p0 – p’) = K (13.b)
Podemos tomar E = K + m0.c² e substituir em (2.a) e obter:
(K + m0.c²)² = c².pe² + (m0.c²)² (14.a)
Desenvolvendo esta expressão, obtemos:
K² + 2.K.m0.c² + m0².c4 = c².pe² + m0².c4 (14.b)
Que, simplificando, dá:
K² + 2.K.m0.c² = c².pe² (14.c)
Dividindo por c²:
K²/c² + 2.K.m0 = pe² (14.c)
Inserimos a energia cinética da equação (13.b) e p² da equação (11.a) nesta última, e então obtemos:
c².(p0 – p’)²/c² + 2.m0.c.(p0 – p’) = p0² + p’² – 2.p0.p’.cosθ (15.a)
Que se reduz a:
(p0 – p’)² + 2.m0.c.(p0 – p’) = p0² + p’² – 2.p0.p’.cosθ (15.b)
Desenvolvemos os termos:
p0² – 2.p0.p’ + p’² + 2.m0.c.(p0 – p’) = p0² + p’² – 2.p0.p’.cosθ (15.c)
Cancelamos os termos semelhantes:
– 2.p0.p’ + 2.m0.c.(p0 – p’) = – 2.p0.p’.cosθ (15.c)
Passando o termo – 2.p0.p’ para o lado direito e dividindo por 2, obtemos:
m0.c.(p0 – p’) = p0.p’(1 – cosθ) (15.d)
Podemos melhorar esta expressão, dividindo tudo por m0.c.p0.p’, e obtemos:
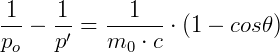
Multiplicando por h e aplicando as equações (3.b) e (3.d) obtemos uma expressão conhecida como a equação de Compton.
λ’ – λ0 = (h/m0.c).(1 – cosθ)
O termo h/m0.c é denominado comprimento de onda de Compton do elétron, designado por λc. Seu valor numérico é obtido substituindo os valores numéricos da constante de Planck h, da massa de repouso do elétron m0 e da velocidade da luz c, de forma que se obtém:
λc = h/m0.c = 2,43x10-12m
O termo λ’ – λ0 = Δλ é denominado deslocamento Compton, e depende do ângulo de desvio em relação à direção do fóton incidente, e é independente do comprimento de onda inicial.
Os resultados de Compton resultam geram o gráfico de Δλ versus θ, representado a seguir:

Figura 02: resultados de compton para o deslocamento compton, em fução do ângulo de espalhamento.
Referências bibliográficas:
EISBERG, Robert RESNICK, Robert. Física Quântica – Átomos, Moléculas, Sólidos, Núcleos e Partículas. Tradução de Paulo Costa Ribeiro, Ênio Costa da Silveira e Marta Feijó Barroso. Rio de Janeiro:Campus, 1979
Texto originalmente publicado em https://www.infoescola.com/fisica/efeito-compton/