Dizemos que um objeto está se movimento quando este, ao longo do tempo, muda sua posição em relação ao observador. Essa relação de deslocamento e tempo de deslocamento chamamos de velocidade.
Se, ao longo do tempo, este corpo continua se movendo com a mesma velocidade, falamos que seu movimento é uniforme. Assim, a cada intervalo igual de tempo, seu deslocamento espacial será o mesmo. Assim, movimento retilíneo uniforme (MRU) é descrito como um movimento de um móvel em relação a um referencial, movimento este ao longo de uma reta de forma uniforme, ou seja, com velocidade constante.

Sabendo que, para haver o movimento, as duas constantes (variação de espaço e variação de tempo) são diferentes de zero.
Variação de espaço (ΔS): diferença entre a posição ocupada pelo objeto no instante final (Sf) de observação e no instante inicial (Si).

Variação de tempo (Δt): diferença entre o instante final (tf) de observação e no instante inicial (ti).

A velocidade calculada dessa forma é chama de velocidade média porque entre o intervalo de tempo usado, a variação do espaço pode ocorrer de formas diferentes do final ou do inicial. Por exemplo, se realizamos uma viagem de 80 km em 1 hora, podemos falar que a velocidade média nesse intervalo de tempo foi de 80 km/h. Mas sabemos que durante esse trajeto o carro andou em alguns momentos a velocidade maior que esse e com velocidade menor em outros. No entanto, se aproximarmos os instantes final e inicial cada vez mais, maiores são as chances de o espaço sofrer variações cada vez menor. Assim, o Δt fica cada vez menor, cada vez mais próximo de 0 (mas nunca sendo 0, em absoluto). Teremos então a velocidade escalar instantânea.
Velocidade média:

Velocidade instantânea:

(lê-se limite de Δt tendendo a zero)
Se pegarmos a relação da velocidade:

E a colocarmos em outro formato, levando em conta as variações de espaço e tempo, temos:

Considerando ti, tempo inicial, como zero:

Eis a função horária do espaço chamada assim pois, sabendo a velocidade e a posição inicial de um corpo, podemos prever sua posição final ao longo do tempo.
O movimento que um corpo descreve pode ser classificado de acordo com a sua orientação em relação à trajetória percorrida.
Movimento progressivo: quando o corpo está se movendo no mesmo sentido que a trajetória.

Objeto e trajetória no mesmo sentido.
Assim, a posição ocupada pelo corpo aumenta com o tempo e a velocidade escalar é positiva.
Movimento retrógrado: quando o corpo está se movendo no sentido contrário a direção da trajetória.
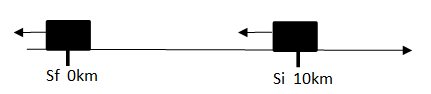
Objeto e trajetória em sentidos opostos.
Nesse caso, a posição ocupada pelo corpo diminui com o tempo e a velocidade escalar é negativa.
Se produzirmos um gráfico dessa equação, uma das possibilidades é esta:
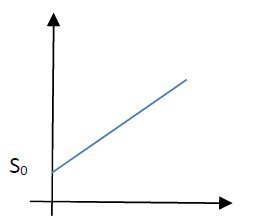
O gráfico acima descreve um corpo com velocidade positiva. Perceba que quando começamos a marcar o tempo (t = 0) o corpo não está no ponto 0 como posição inicial (S0 – diferente de zero).
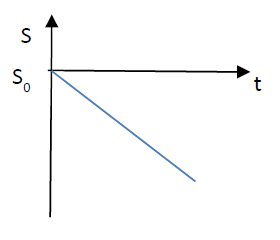
Aqui, um exemplo de velocidade negativa. Também contrário ao gráfico anterior, o corpo inicia o movimento junto com a contagem de tempo, então, a posição inicial é zero e segue no sentido contrário à trajetória (posição negativa) caracterizando um movimento retrógrado.
Exemplo
Um determinado móvel esta se deslocando em uma trajetória retilínea (MRU) segundo a função horária S = 4+28t. Pede-se:
- a) Determinar seu espaço inicial (So).
- b) A velocidade do móvel no instante t = 2s.
- c) O espaço do móvel no instante t=3s.
- d) A variação de espaço nos 5 primeiros segundos.
Resolução
- a) Como S = So + v.t e temos S = 4 + 28t , S0 = 4 m
- b) Como o móvel está em MRU, sua velocidade é constante . Se S = S0+ v.t e temos S = 4+28t, v = 28 m/s
- c) S = 4+28t, para t = 3s basta substituirmos, S = 4+28.3 = 88m
- d) Basta acharmos S5. Pela função temos S5 = 4+28.5 = 144m
Referências:
Os Fundamentos da Física – Moderna Plus. Ramalho, Nicolau e Toledo. Vol. 01. Moderna. 11ª Ed. SP. 2016
Texto originalmente publicado em https://www.infoescola.com/fisica/movimento-retilineo-uniforme/