Movimento Uniformemente Variado (MUV)

Dizemos que um objeto está se movimentando quando este, ao longo do tempo, muda sua posição em relação ao observador. Essa relação de deslocamento e tempo de deslocamento chamamos de velocidade.

Se, ao longo do tempo, este corpo continua se movendo com a mesma velocidade, falamos que seu movimento é uniforme. No entanto, sabemos que a velocidade também pode mudar a cada instante que observamos. Se a cada instante sua velocidade aumenta ou diminui de forma uniforme, eis o que chamamos de movimento uniformemente variado (MUV).

A taxa com a qual a velocidade varia no tempo é chamada de aceleração.

Assim, temos:

Aceleração média (a_m): razão entre variação da velocidade (Δv) e o tempo (Δt) em que ocorreu essa variação.

$a_m = \frac{\Delta v}{\Delta t}$

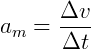
Agora, observando a trajetória que o corpo descreve, ele pode ter 4 definições.

Movimento progressivo

Quando o corpo está se movendo no mesmo sentido que a trajetória. Se o módulo da velocidade aumenta com o tempo, temos um movimento acelerado progressivo. Caso contrário, o módulo da velocidade diminui com o tempo, chamamos de movimento retardado progressivo.

Objeto e trajetória no mesmo sentido

Movimento acelerado progressivo

|V₂ |> |V₁| velocidade aumenta com o tempo.

Movimento retardado progressivo

|V₂| < |V₁| velocidade diminui com o tempo.

Movimento retrógrado

Quando o corpo está se movendo no sentido contrário a direção da trajetória. Neste caso, se o módulo da velocidade aumenta com o tempo, temos um movimento acelerado retrógrado. E, caso o módulo da velocidade diminui com o tempo, chamamos de movimento retardado retrógrado.

Objeto e trajetória em sentidos opostos

Movimento acelerado retrógrado

|V₂| > |V₁| velocidade aumenta com o tempo.

Movimento retardado retrógrado

|V₂| < |V₁| velocidade diminui com o tempo.

Perceba que, como a variação de velocidade pode ser positiva ou negativa, a aceleração vai assumir esses valores positivo ou negativo em função da velocidade. Uma vez que a variação do tempo é sempre positiva.

Da relação da aceleração, temos:

$a_m = \frac{\Delta v}{\Delta t}$

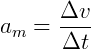
Se trabalharmos as variações de velocidade e tempo, temos:

$a_m = \frac{v - v_0}{t - t_0}$

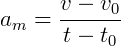
Considerando t₀, tempo inicial, como zero:

$v = v_0 + a \cdot t$

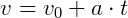
Esta equação é denominada função horária da velocidade. Perceba que podemos descobrir a velocidade (v) de um certo corpo, para cada instante (t) de sua trajetória.

Se produzirmos um gráfico dessa equação, uma das possibilidades é esta:

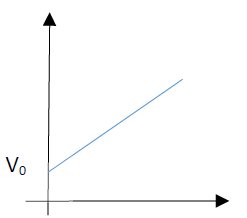
O gráfico acima descreve um corpo com aceleração positiva. Perceba que quando começamos a marcar o tempo (t = 0) o corpo já estava em movimento (velocidade inicial – v₀ – diferente de zero).

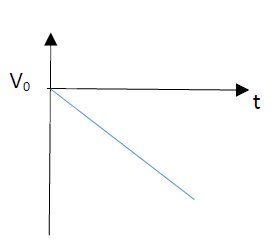
Aqui, um exemplo de aceleração negativa. Também contrário ao gráfico anterior, o corpo inicia o movimento junto com a contagem de tempo, então, velocidade inicial é zero e segue no sentido contrário ao sentido (velocidade negativa) caracterizando um movimento retrógrado retardado.

A partir da função horária da velocidade e do gráfico que ela produz (discutido acima), podemos chegar em outra função horária – a do espaço.

$S = S_0 + v_0 \cdot t + \frac{a}{2} \cdot t^2$

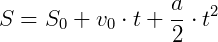
Ou seja, da mesma forma que a velocidade varia com o tempo (t), a posição (S) - o espaço que o corpo ocupa no tempo - também varia de sua posição inicial (S_o).

Existem casos em que temos informações sobre a trajetória do corpo, mas não temos como saber há quanto tempo ele está em movimento. Assim, ao unirmos as duas funções horárias, temos:

$v^2 = v_{0}^2 + 2 \cdot a \cdot \Delta S$

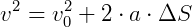
Esta é a Equação de Torricelli para o Movimento Uniformemente Variado (MUV) e descreve a velocidade de um corpo em função da sua trajetória. Perceba que precisamos saber a orientação da trajetória para saber se a velocidade será positiva ou negativa.

Texto originalmente publicado em https://www.infoescola.com/fisica/movimento-uniformemente-variado-muv/