Velocidade angular

No movimento uniforme (MU) ou no movimento uniformemente variado (MUV) estudamos uma trajetória linear. No entanto, é possível que um corpo se mova em uma trajetória circular, determinando ângulos ao longo do caminho.

Trajetória linear.

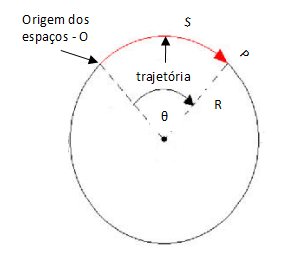
Na imagem acima, um ponto realizou uma trajetória do ponto O ao ponto P descrevendo um espaço linear S e um espaço angular θ em um círculo de raio R. O ângulo θ é dado em radianos e se relaciona com o espaço linear descrito e o raio R do círculo.

$S = \theta R$

Ou

$\theta = \frac{S}{R}$

Da relação acima, perceba que uma grandeza linear por ser relacionada a uma grandeza angular.

Velocidade angular média (ω_m)

Assim como a velocidade linear, é a relação entre a variação de espaço angular em determinado tempo.

Ficou-se convencionado que a trajetória do movimento se dá no sentido horário. Assim, o movimento que seguir essa orientação será positivo e a que for o contrário, negativo.

$\omega_m = \frac{\Delta\theta}{\Delta t}$

Velocidade angular instantânea (ω)

Quando a variação do tempo de trajetória tende a 0.

$\omega = \underset{\Delta t \to 0}{\lim} \frac{\Delta\theta}{\Delta t}$

(lê-se limite de Δt tendendo a zero)

Da velocidade angular média, temos:

$\omega_m = \frac{\theta_f - \theta_i}{t_f - t_i}$

Considerando t_i, tempo inicial, como zero:

$\theta = \theta_i + \omega t$

Da relação entre espaço linear e angular, mencionada no início do texto, temos:

$\theta = \frac{S}{R}$

Também podemos usar essa relação para a variação de espaços:

$\Delta\theta = \frac{\Delta S}{R}$

$\Delta\theta R = \Delta S$

Para a velocidade, temos:

$\frac{\Delta\theta R}{\Delta t} = \frac{\Delta S}{\Delta t}$

$\omega R = v$

Então:

$v = \omega R$

Ou

$\omega = \frac{v}{R}$

Referências:

Os Fundamentos da Física – Moderna Plus. Ramalho, Nicolau e Toledo. Vol. 01. Moderna. 11ª Ed. SP. 2016

Texto originalmente publicado em https://www.infoescola.com/fisica/velocidade-angular/