Área de um Triângulo

Conteúdo deste artigo

O que é um triângulo?
Cálculo da área de um triângulo
Altura de um triângulo
Triângulo equilátero
Outros métodos para cálculo de áreas de triângulos

O que é um triângulo?

O triângulo é uma das figuras geométricas mais simples que existem. Apesar disso, foi alvo de inúmeros estudos no decorrer do desenvolvimento da Matemática ao redor do mundo. O estudo mais conhecido, talvez, é o Teorema de Pitágoras.

Cálculo da área de um triângulo

Área é o espaço interno de qualquer figura geométrica plana. A área de um triângulo pode ser calculada de diversas formas, utilizando conceitos e métodos diferentes. Existe uma fórmula (modelo matemático) que nos fornece a área de um triângulo qualquer, sabendo apenas a medida da base e da altura desse triângulo. Essa fórmula é a seguinte:

$A = \frac{\text{base }\times \text{altura}}{2} = \frac{b \cdot h}{2}$

Onde b é a medida da base do triângulo e h a sua altura.

Assim como tudo na matemática, nada cai do céu. Existe uma demonstração simples que mostra como obtemos esta fórmula.

Imagine um retângulo qualquer de base b e altura h:

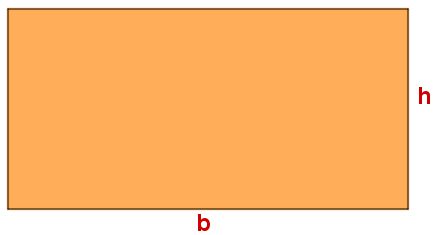
Encontramos a área desse retângulo multiplicando a base pela altura, ou seja, $A = b \cdot h$

Agora vamos traçar uma diagonal. Veja que teremos dois triângulos:

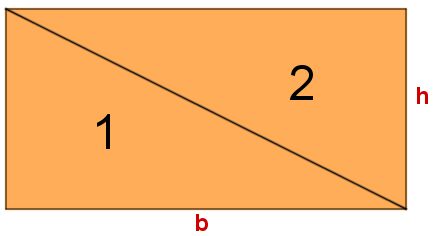
Como traçamos uma diagonal, dividimos o retângulo em duas metades iguais. Com isso, criamos dois triângulos idênticos, ou seja, de mesma área. A área de cada triângulo será metade da área do retângulo, ou seja, se a área do retângulo é $A = b \cdot h$ , a área de cada triângulo será essa área dividida por dois, ou seja, $A = \frac{b \cdot h}{2}$ .

Altura de um triângulo

A altura de um triângulo é o segmento que liga um ponto a seu segmento oposto (base oposta), formando com ele um ângulo de 90°. Dizemos que a altura de um triângulo é sempre perpendicular à sua base.

Devemos tomar um certo cuidado para encontrar a altura de um triângulo. Dependendo do seu tipo, muitas vezes essa altura não é visível facilmente.

Se o triângulo for acutângulo, onde todos os ângulos internos são agudos (menores que 90°), teremos uma altura “dentro” do triângulo, independente se ele é escaleno, isósceles ou equilátero.

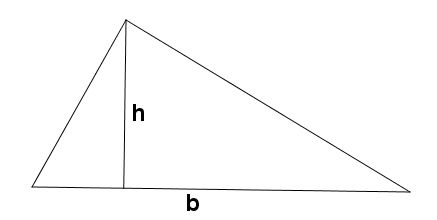
Se o triângulo for obtusângulo, onde um de seus ângulos internos é obtuso (maior que 90°), teremos uma altura “fora” do triângulo, dependendo de qual lado escolhermos como base. Vamos considerar o triângulo ABC:

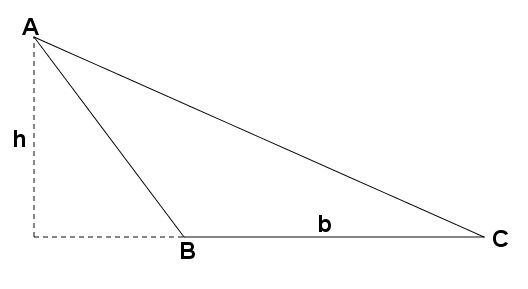Como escolhemos como base o segmento BC, tivemos que prolongar esse segmento para a esquerda e traçar a altura com origem no ponto A, perpendicular a esse prolongamento do segmento BC.

Se por acaso escolhermos AC como base, a altura ficará “dentro” do triângulo ABC, veja:

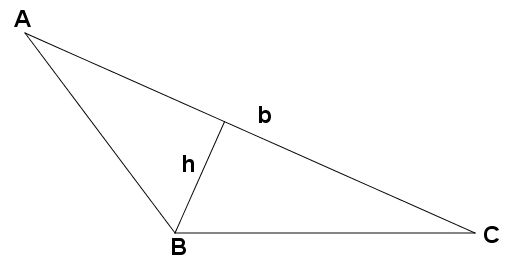
Por isso vale ressaltar que a base de um triângulo não é somente a que estiver “apoiada ao chão”. Podemos escolher qualquer lado como base.

Se o triângulo for retângulo (um de seus ângulos mede 90°), a altura será igual a um de seus catetos, desde que a base seja o outro cateto.

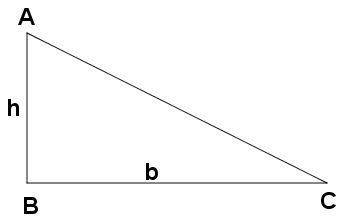
Triângulo equilátero

Em um triângulo equilátero (triângulo onde todos os seus lados têm a mesma medida), o cálculo da área pode ser facilitado, precisando, para isso, apenas do valor da medida do lado desse triângulo. Vamos deduzir uma fórmula para isso, considerando o triângulo equilátero ABC, a seguir, de medida a.

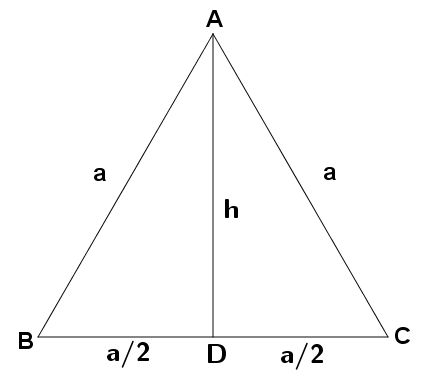
Vamos nos concentrar em um dos triângulos retângulos que foram formados: ABD e ACD.

Em ABD, vamos aplicar o Teorema de Pitágoras.

$a^2 = h^2 + \left(\frac{a}{2}\right)^2$

$a^2 = h^2 + \frac{a^2}{4}$

$h^2 = a^2 - \frac{a^2}{4}$

$h^2 = \frac{3a^2}{4}$

$h = \sqrt{\frac{3a^2}{4}}$

$h = \frac{a\sqrt{3}}{2}$

Agora, como a área de um triângulo qualquer é: $A = \frac{b \cdot h}{2}$ , teremos:

$A = \frac{a \cdot \left(\frac{a\sqrt{3}}{2}\right)}{2} = \frac{a^2\sqrt{3}}{2} \cdot \frac{1}{2} = \frac{a^2\sqrt{3}}{4}$

Assim, em todo triângulo equilátero em que se conhece a medida de seu lado, para encontrar a sua área basta utilizar a fórmula $A = \frac{a^2\sqrt{3}}{4}$ .

Exemplo: Qual a área de um triângulo equilátero que mede 8 cm de lado?

Resposta: $A = \frac{a^2\sqrt{3}}{4} = \frac{8^2\sqrt{3}}{4} = \frac{64\sqrt{3}}{4} = 16\sqrt{3} \text{ cm }^2$

Outros métodos para cálculo de áreas de triângulos

Existem ainda outras técnicas para calcular a área de um triângulo. Uma delas consiste em calcular da área de um triângulo, conhecendo um de seus ângulos e as medidas dos lados que formam esse ângulo. A fórmula é a seguinte:

$A = \frac{1}{2} \cdot a \cdot b \cdot \text{sen } \alpha$

Onde temos as medidas de dois lados, a e b, e $\alpha$ o ângulo formado por esses lados.

Exemplo: calcular a área do seguinte triângulo:

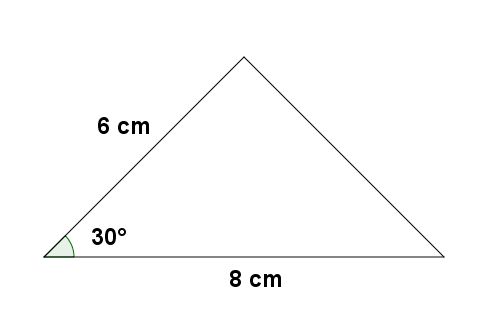Utilizando a fórmula teremos:

$A = \frac{1}{2} \cdot 6 \cdot 8 \cdot \text{sen }30^o$

$A = \frac{1}{2} \cdot 48 \cdot \frac{1}{2}$

$A = \frac{48}{4}$

$A = 12 \text{ cm}^2$

É possível encontrar a área de um triângulo apenas com as medidas de seus três lados. Para isso existe a fórmula de Herão (ou de Heron). A fórmula é a seguinte:

$A = \sqrt{p(p-a)(p-b)(p-c)}$