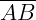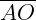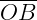Conteúdo deste artigo
Círculo
Podemos definir um círculo como sendo o conjunto de todos os pontos interiores de uma circunferência, ou seja, é o espaço contido dentro da circunferência.
Todo círculo ou circunferência possui alguns elementos importantes:
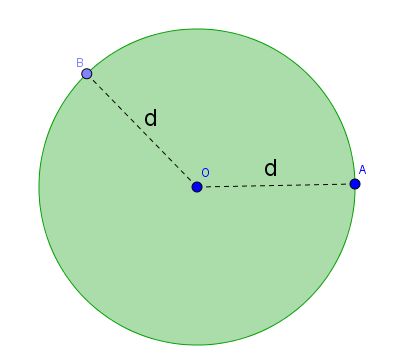
- O é o centro da circunferência;
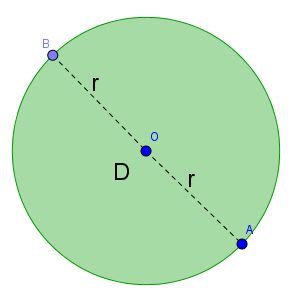
 é o Diâmetro (D);
é o Diâmetro (D); e
e  são raios (r);
são raios (r);
Setor circular
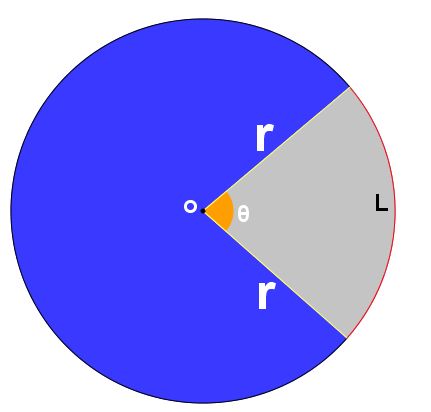
Um setor circular é uma região do círculo delimitada por dois de seus raios, partindo do centro e um arco:
Usualmente podemos chamar um setor circular de “fatia de pizza”, pelo seu formato. O ângulo 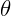 é chamado de ângulo central.
é chamado de ângulo central.
De acordo com seu ângulo, um setor circular pode ser classificado como:
Metades: quando o ângulo central mede 180°
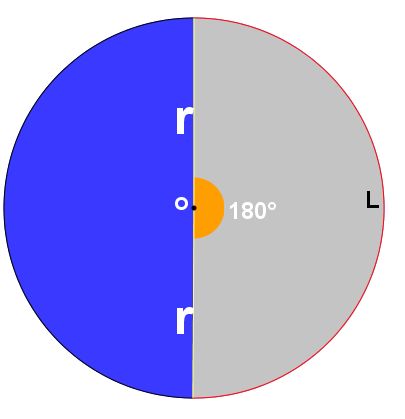 Quadrantes: quando o ângulo central mede 90°
Quadrantes: quando o ângulo central mede 90°
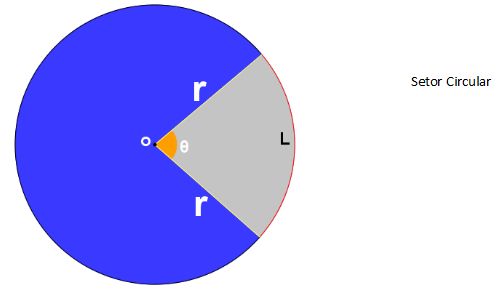
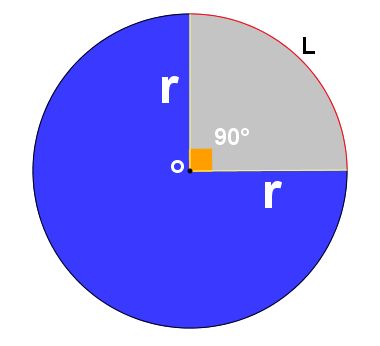 Oitantes: quando o ângulo central mede 45°:
Oitantes: quando o ângulo central mede 45°:
 Área em função do ângulo central
Área em função do ângulo central
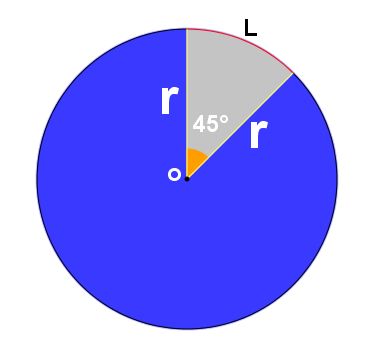
Seja um setor circular de raio r = 4 cm e ângulo central 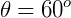 .
.
Para calcular a área, devemos ter a medida do ângulo central e a medida do raio, como está na figura.
Devemos pensar: "a área do setor de ângulo 60° e raio 4 cm corresponde a que fração da área do círculo inteiro?"
Também devemos pensar: "60° corresponde a que fração de 360°?"
Isso porque a fração que 60° corresponde em relação a 360° é a mesma fração que a área do setor corresponde em relação a área total do círculo.
Assim, teremos a seguinte relação:
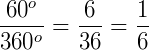
Ou seja, 60° é  de 360º. Isso quer dizer que a área do setor circular também será
de 360º. Isso quer dizer que a área do setor circular também será  da área total do círculo. Lembrando que a área de um círculo é dada por
da área total do círculo. Lembrando que a área de um círculo é dada por 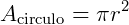 , teremos:
, teremos:
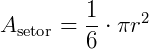
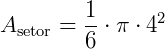
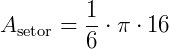
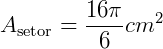
Substituindo 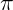 por 3,14, teremos:
por 3,14, teremos:
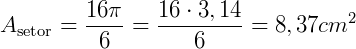
Lembrando que o valor de 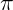 , usualmente é 3,14. Mas há alguns casos onde o exercício pode pedir para que se adote
, usualmente é 3,14. Mas há alguns casos onde o exercício pode pedir para que se adote 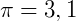 ou mesmo
ou mesmo 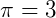 . Também pode ocorrer que se peça com mais casas decimais.
. Também pode ocorrer que se peça com mais casas decimais.
Encontrando uma fórmula
Vamos generaliza uma fórmula para calcularmos a área de um setor circular.
Como a fração que o ângulo central corresponde em relação a 360° é a mesma fração que a área do setor corresponde em relação a área total do círculo, podemos fazer:
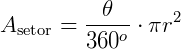
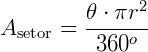
Isso considerando que o ângulo está dado em graus. Caso a medida do ângulo esteja em radianos, teremos que 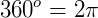 , então:
, então:
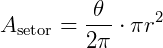
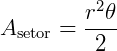
Para entender esta fórmula podemos usar uma proporção simples, pois a razão entre o ângulo do setor e 360° é a mesma que a área do setor e a área total:
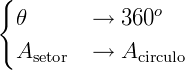
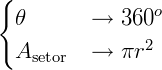

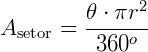
Área em função do comprimento do arco
É possível determinar a área de um setor circular sabendo o comprimento do arco que o delimita.
Primeiro, vamos lembrar como se calcula o comprimento de um arco através de uma simples proporção.
Imaginemos um círculo de raio r, ângulo 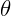 e arco L .
e arco L .
O comprimento do círculo todo, com um ângulo de 360°, é o mesmo que o comprimento de uma circunferência, ou seja, 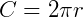 .
.
Queremos saber qual o comprimento de um arco, cujo ângulo é 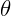 . Assim, temos:
. Assim, temos:
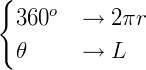
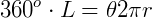
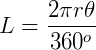
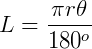
Já sabemos que a área do setor será: 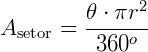 .
.
Vamos isolar 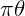 na fórmula do comprimento do arco L, para substituir na fórmula da área do setor.
na fórmula do comprimento do arco L, para substituir na fórmula da área do setor.
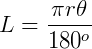
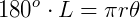
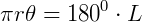
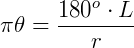
Substituindo na fórmula da área do setor, teremos:
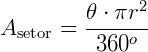
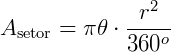
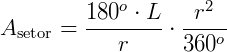
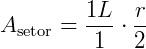
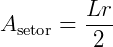
Assim, a área de um setor circular também pode ser obtida, sabendo apenas o raio e a medida do arco que o delimita, sem necessidade do ângulo.
Exemplos:
1. Calcule a área de um setor circular, sabendo que o seu raio mede 5 cm e que o seu ângulo central mede 45°. (Adote 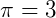 ).
).
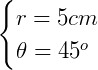
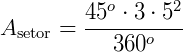
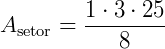
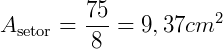
2. Qual a área de um setor cujo arco mede 30 cm, com raio igual a 7 cm?
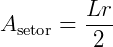
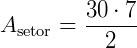
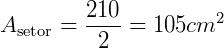
Referências:
DANTE, Luiz Roberto. Matemática: contexto & aplicações. 2. ed. São Paulo: Ática, 2013.
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.
RIBEIRO, Paulo Vinícius. Matemática: Áreas de círculo e suas partes. Vol. 5. São Paulo: Bernoulli.
Texto originalmente publicado em https://www.infoescola.com/matematica/area-de-setores-circulares/