Conteúdo deste artigo
O que é um losango?
O losango é um quadrilátero (polígono de quatro lados) cuja medida de seus lados são iguais. Além disso, possui dois ângulos opostos obtusos (maiores que 90°) outros dois ângulos opostos agudos (menores que 90°). Em todo losango, as diagonais são bissetrizes (dividem os ângulos em dois outros de mesma medida) e são retas perpendiculares (formam um ângulo de 90° entre si).
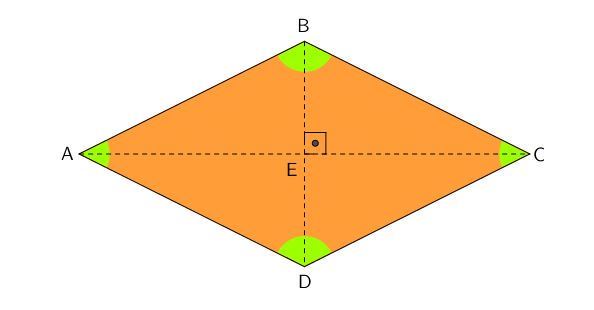
Todo losango possui duas diagonais, ligando seus vértices opostos.
Quando o losango apresenta dois ângulos agudos e dois obtusos, as diagonais têm tamanhos diferentes, ou seja, há uma diagonal maior D e outra menor d.
Quando o losango apresenta seus quatro ângulos iguais (caso em que todos os ângulos possuem 90°) temos, então, um quadrado, e as suas diagonais são todas de igual comprimento.
Área de um losango
Área é o espaço interno de qualquer figura geométrica plana.
Uma das maneiras de calcular a área de um losango é multiplicando-se as suas diagonais e dividindo o resultado obtido pela metade, veja:
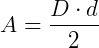
Onde D é a medida da diagonal maior e d a medida da diagonal menor.
Existe uma demonstração que mostra como obtemos esta fórmula.
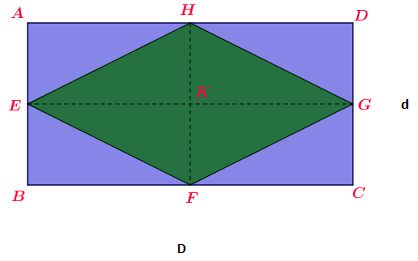
Imagine um losango qualquer. Em seguida, vamos construir um retângulo em volta dele.
Teremos, então, um retângulo ABCD e, dentro dele, o losango EFGH, com diagonal maior EG (D) e diagonal menor HF (d).
Como se trata de um retângulo, a sua área será 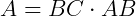 . Como BC = EG = D e AB = HF = d, a área será
. Como BC = EG = D e AB = HF = d, a área será 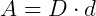 .
.
Observe que o retângulo ABCD está dividido em 4 retângulos menores. Em cada um desses retângulos, há duas regiões: uma correspondente ao retângulo maior e outra referente ao losango. Observe que essas duas partes são duas metades. Ou seja, se juntarmos a área de todas as partes em azul, essa área será metade da área do retângulo maior, fazendo com que a área do losango seja a outra metade do retângulo. Assim, a área do losango será metade da área do retângulo que está a sua volta, ou seja, 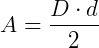 .
.
Outro método para encontrar a fórmula da área
Considere o retângulo EBFK. Nele, vamos calcular a área do triângulo verde EKF.
Nesse triângulo, a base será 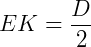 e a altura será
e a altura será 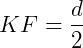 .
.
Então a área de EKF será:
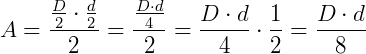
A área do losango é formada por 4 áreas iguais a área do triângulo EKF, assim, vamos multiplicar o resultado encontrado por 4.
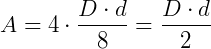
Exemplos:
Calcule a área de um losango que possui diagonal maior medindo 10cm e diagonal menor medindo 7cm:
Temos que
- D = 10 cm
- d = 7 cm
Aplicando a formula:
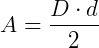
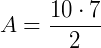
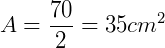
Encontre a medida da diagonal maior de um losango que apresenta área igual a 60 m², sabendo que a diagonal menor mede 6m:
Vamos aplicar a fórmula encontrada:
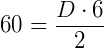
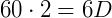
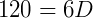
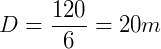
Referências:
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.
RIBEIRO, Paulo Vinícius. Matemática: Teorema de Tales e quadriláteros. Vol. 2. São Paulo: Bernoulli.
Texto originalmente publicado em https://www.infoescola.com/matematica/area-de-um-losango/