Combinação simples

O princípio multiplicativo é a ferramenta básica utilizada para resolver problemas de contagem. Sua aplicação direta na resolução de problemas pode às vezes tornar-se trabalhosa. Percebemos, contudo, que alguns problemas possuem características em comum e são recorrentes. Iremos a seguir, definir o agrupamento chamado Combinação Simples.

O que é uma combinação simples?

Se um conjunto A tem n elementos, a combinação simples de p elementos escolhidos entre esses n elementos dados (p ≤ n) é qualquer subconjunto de A com p elementos.

Indica-se: 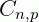$C_{n,p}$ ou $C_{n}^{p}$

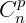
Exemplo:

Suponha que os estudantes Andreia, Bernardo, Caio, Daniel e Érica disputam duas vagas no conselho da escola. Quantas comissões de 2 estudantes podemos formar escolhendo entre os 5 estudantes?

Responder a essa pergunta é o mesmo que calcular quantos subconjuntos de dois elementos podem ser formados com os 5 elementos do conjunto: {A, B, C, D e E}. Cada um desses subconjuntos é uma combinação simples de 2 elementos escolhidos entre os cinco elementos dados.

Observem as possíveis combinações no diagrama de árvore abaixo:

São ao todo comissões com 2 estudantes. Podemos notar que, dado um conjunto de 5 elementos, o número de subconjuntos com 2 elementos é metade (½) do total dos agrupamentos de 2 elementos formados com os 5 algarismos disponíveis. Isto se deve ao fato de, por exemplo, os agrupamentos {A,B} ; {B, A} serem iguais, enquanto {A, B} e {C, B} são diferentes.

Quando, pelo princípio multiplicativo, indicamos 5 . 4 = 20, estamos considerando a ordem dos elementos. Como na formação de subconjuntos a ordem dos elementos não importa, devemos dividir o resultado anterior por 2 = 2 . 1 = 2!, isto é, devemos dividir pela permutação de 2, que é o número de elementos em cada subconjunto.

Generalizando, podemos dizes que o princípio multiplicativo leva em conta a ordem dos elementos do grupo formado. Se essa ordem não importar, devemos excluir as repetições dividindo o resultado, obtido com o princípio multiplicativo, pelo número de permutações dos componentes do grupo.

Cálculo do número de Combinações simples

$C_{n}^{p}=C_{n,p}=\frac{n!}{(n-p)!\cdot p!}$

Exercícios resolvidos

1º) Uma empresa é formada por 6 sócios brasileiros e 4 japoneses. De quantos modos podemos formar uma diretoria de 5 sócios, sendo 3 brasileiros e e 2 japoneses?

Resolução:

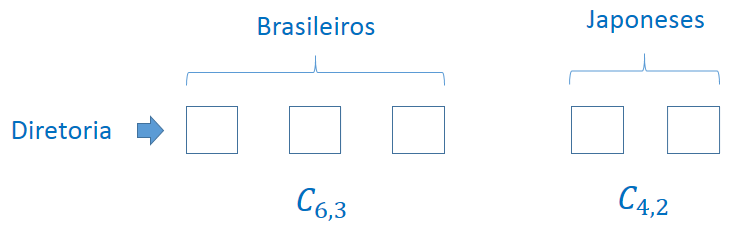
Resposta:

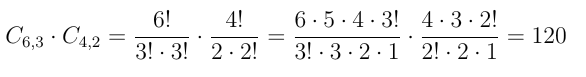
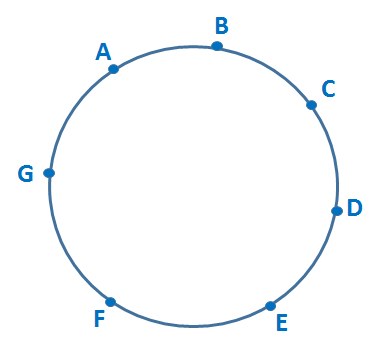
2º) Sobre uma circunferência tomam-se 7 pontos distintos. Calcule o número de polígonos convexos que se pode obter com vértices nos pontos dados.

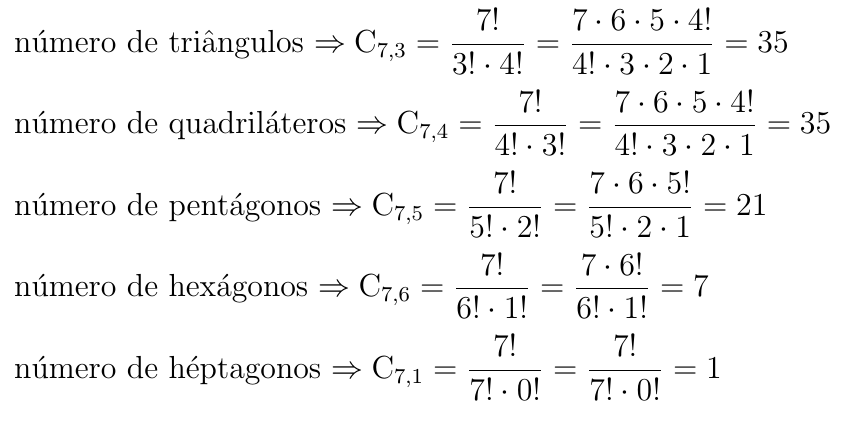
Logo, o total de polígonos é: 35 + 35 + 21 + 7 + 1 = 99

3º) Considere, num plano, 10 pontos distintos entre si. Suponha que 4 desses pontos pertençam a uma mesma reta e que 2 quaisquer dos demais não estejam alinhados com nenhum dos pontos restantes. Calcule o número de retas determinadas por esses 10 pontos.

Resolução:

Admitindo-se que o alinhamento de 3 pontos do total de 10 só seja possível entre os 4 pontos da reta dada, temos:

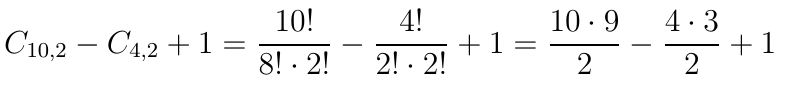
Logo, o resultado final é: 45 – 6 + 1 = 40

4º) Um baralho tem 52 cartas. De quantos modos diferentes podemos distribuí-las entre 4 jogadores de modo que cada um receba 13 cartas?

Resolução:

Referências bibliográficas:

1. MORGADO, Augusto C.; CARVALHO, João B. P. de; CARVALHO, Paulo Cezar P.; FERNANDEZ, Pedro – Análise Combinatória e Probabilidade – 9ª ed. – Rio de Janeiro, SBM, 1991

2. SANTOS, José Plínio O.; MELL, Margarida P.; MURARI, Idani T. C. – Introdução à Análise Combinatória – 4ª edição revista – Rio de Janeiro: Editora Ciência Moderna, 2007.

3. LIMA, Elon Lages. A Matemática do Ensino Médio. Volume 2, 6.ed. Coleção do Professor de Matemática. Rio de Janeiro: SBM, 2006.

Texto originalmente publicado em https://www.infoescola.com/matematica/combinacao-simples/