Divisão de frações

Dividir frações é tão simples quanto multiplicar. Já sabemos que frações são números representados na forma de uma razão entre de dois números inteiros ou que simbolizam uma proporção. Por exemplo, se dividirmos uma pizza em 8 pessoas, cada uma delas recebeu igualmente de $\frac{1}{8}$ uma pizza.

Para dividirmos as frações basta multiplicarmos a fração que está no numerador pelo inverso da fração que está no denominador. Veja abaixo a regra:

$\frac{a}{b}\cdot\frac{c}{d}=\frac{a\cdot d}{b\cdot c}$

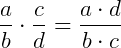
Ou também podemos escrever:

$\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a\cdot d}{b\cdot c}$

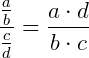
Se uma fração estiver dividindo um número a, temos:

$a\div\frac{b}{c}=\frac{a}{\frac{b}{c}}=\frac{a}{1}\cdot\frac{c}{b}=\frac{a\cdot c}{b}$

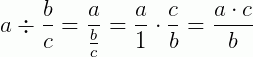
E se um número divide uma fração:

$\frac{b}{c}\div a=\frac{\frac{b}{c}}{a}=\frac{b}{c}\cdot\frac{1}{a}=\frac{b}{c\cdot a}$

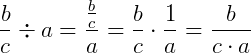
Exemplo 1)

$\frac{2}{3}\div\frac{5}{7}=\frac{\frac{2}{3}}{\frac{5}{7}}=\frac{2\cdot 7}{3\cdot 5}=\frac{14}{15}$

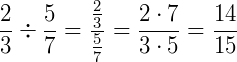
Exemplo 2) Veja abaixo uma divisão de um número por uma fração:

$5\div\frac{4}{3}=\frac{5}{\frac{4}{3}}=\frac{5\cdot 3}{4}=\frac{15}{4}$

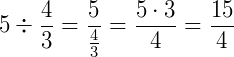
Exemplo 3) Note a diferença. Este caso é o contrário do exemplo 2:

$\frac{4}{3}\div 5=\frac{\frac{4}{3}}{5}=\frac{4}{3\cdot 5}=\frac{4}{15}$

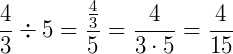
Referências Bibliográficas

DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/divisao-de-fracoes/