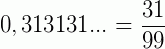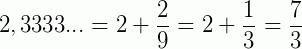Conteúdo deste artigo
- Forma decimal dos números racionais
- Como obter a fração geratriz equivalente à uma dízima periódica
- Dízima periódica simples
- Método prático para obter a fração geratriz de uma dízima periódica simples
- Dízimas periódicas compostas
- Método prático para obter a fração geratriz de uma dízima periódica composta
Forma decimal dos números racionais
Todo número racional resulta da divisão de dois inteiros. Essa razão ou é um número inteiro ou pode ser escrita na forma de número decimal.
Temos três casos a considerar:
1º) o denominador da fração apresenta, na forma irredutível, apenas os fatores primos 2 ou 5; neste caso, obtemos um número decimal exato, ou seja, com um número finito de casas decimais.
Exemplos:
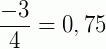
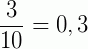
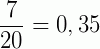
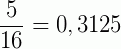
*Nesse caso, observe que os denominadores das frações (irredutíveis) apresentam apenas 2 e 5 como fatores primos.
2º) o denominador da fração não apresenta, na forma irredutível, nem o fator 2 nem o fator 5; obtemos, neste caso, uma dízima periódica simples.
Exemplos:
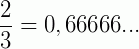
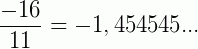
Numa dízima periódica simples, há um número infinito de casas decimais. No entanto, existe um algarismo ou um grupo de algarismos que se repete, logo após a vírgula. A esse algarismo ou grupo de algarismos chamamos período da dízima. Nos exemplos acima, a primeira dízima tem período 6 e a segunda tem período 45.
3º) o denominador da fração apresenta, na forma irredutível, tanto os fatores primos 2 ou 5 como outro(s) fator(es) primo(s) distinto(s) de 2 ou 5; o decimal obtido é, neste caso, uma dízima periódica composta.
Exemplos:
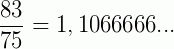
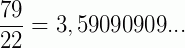
Na dízima periódica composta, há também um número infinito de casas decimais. Além do período (6 e 90 nos dois exemplos acima), aparece agora também uma parte denominada anteperíodo: trata-se do algarismo ou grupo de algarismos que se encontra após a vírgula e antes do período.
Assim, no 1º exemplo acima o anteperíodo é 10 e, no 2º exemplo, o anteperído é 5.
Como obter a fração geratriz equivalente à uma dízima periódica
Dízima periódica simples
Exemplo 1:
Encontrar a fração geratriz da dízima 0,777...
Vamos indicar 0,777... por x:
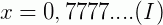
Multiplicamos os dois membros dessa igualdade por 10 para obter outro número na forma decimal com o mesmo período.
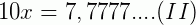
Fazendo, membro a membro, (II) – (I), eliminando a parte que repete.
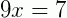
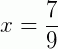
Portanto,  é a fração geratriz equivalente à 0,7777...
é a fração geratriz equivalente à 0,7777...
Exemplo 2:
Encontrar a fração geratriz da dízima 4,151515...
Vamos indicar 4,151515... por x
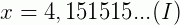
Multiplicamos os dois membros dessa igualdade por 100 para obter outro número na forma decimal com o mesmo período.
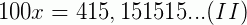
Fazendo, membro a membro, (II) – (I), eliminando a parte que repete.
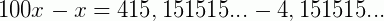
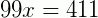
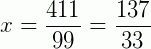
Portanto, 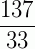 é a fração geratriz equivalente à 4,151515...
é a fração geratriz equivalente à 4,151515...
Método prático para obter a fração geratriz de uma dízima periódica simples
Adicionamos à parte inteira uma fração cujo numerador é o período da dízima e cujo denominador é um número formado por tantos noves quantos são os algarismos do período.
Exemplos:
 (período: 31)
(período: 31) (período: 3)
(período: 3)
Dízimas periódicas compostas
Exemplo:
Encontrar a fração geratriz da dízima 0,04777777...
Vamos indicar 0,04777777... por x
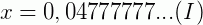
Multiplicamos os dois membros dessa igualdade por 100 para obter outro número na forma decimal com o mesmo período.
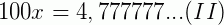
Multiplicamos os dois membros da equação (I) por 1000 para obter outro número na forma decimal com o mesmo período.
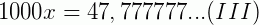
Fazendo, membro a membro, (III) – (II), eliminando a parte que repete.
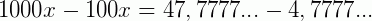
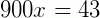
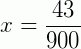
Portanto, 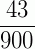 é a fração geratriz equivalente à 0,04777777...
é a fração geratriz equivalente à 0,04777777...
Método prático para obter a fração geratriz de uma dízima periódica composta
Adicionamos à parte inteira uma fração cujo numerador é formado pelo anteperíodo seguido de um período, menos o anteperíodo e cujo denominador é formado de tantos noves quantos são os algarismos do período seguidos de tantos zeros quantos são os algarismos do anteperíodo.
Exemplos:
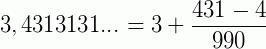
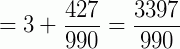
(período: 31; anteperíodo: 4)
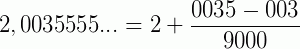
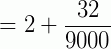
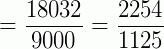
(período: 5; anteperíodo: 003)
Referências bibliográficas:
1. BICUDO, Irineu. Educação Matemática e Ensino de Matemática. Temas e Debates: Sociedade Brasileira de Educação Matemática – SBEM, Ano IV – N.3 – 1991.
2. BOYER, Carl Benjamim. Tópicos de História da Matemática para uso em sala de aula, volume 6. São Paulo: Atual, 1992
3. DANTE, L. R. Projeto Teláris: Matemática. São Paulo: Ática, 2015. v. 2 . 320p.
4. LIMA, E. L. Números e Funções Reais. Rio de Janeiro: SBM: Coleção PROFMAT, Sociedade Brasileira de Matemática, Rio de Janeiro, Brasil, 2013. 297 p.
5. LIMA, Elon Lages: Explorando o ensino da Matemática: artigos: volume 1 Brasília: Ministério da Educação, Secretaria de Educação Básica, 2004. 240 p.
Texto originalmente publicado em https://www.infoescola.com/matematica/dizima-periodica/