Frações algébricas são todas as frações em que variáveis aparecem no denominador ou no numerador da mesma. Elas podem aparecem em um problema onde devemos encontrar os valores dessas variáveis ou apenas como exercício para simplificar uma expressão. Vamos dar alguns exemplos do que seriam frações algébricas:
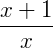
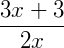
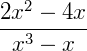
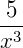
É importante lembrar que uma fração é um número escrito na forma:
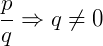
Vamos relembrar algumas propriedades a respeito das operações com frações e em seguida vamos resolver alguns exercícios práticos envolvendo frações algébricas.
Adição e subtração de frações:
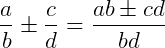
Multiplicação e divisão de frações:
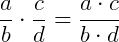
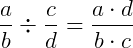
Exemplo 1) Vamos determinar qual é o valor de x na equação abaixo:
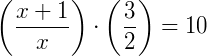
Note que na equação, podemos multiplicar as duas frações do lado esquerdo do membro, onde obtermos:
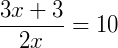
Continuando, temos:
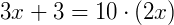
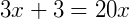
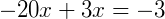
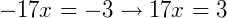
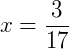
Exemplo 2) Agora, vamos determinar o valor de x na expressão:
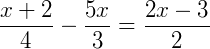
Somando as frações do lado esquerdo da expressão utilizando a propriedade de soma de frações, temos:
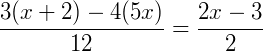
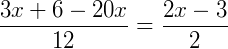
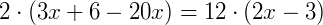
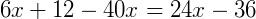
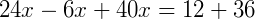
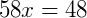
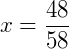
Simplificando a fração obtida acima, obtemos:
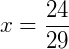
Exemplo 3) Agora vamos descobrir se há uma maneira de reescrever a expressão abaixo. Vale lembrar que neste exemplo o nosso objetivo não é encontrar o valor da variável, e sim reescrever a expressão abaixo de uma forma fatorada:
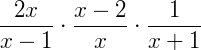
Note é uma multiplicação entre três frações. Então, pela propriedade:
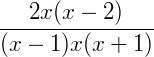
Continuando, temos:
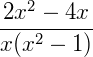
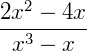
Ou, de outra maneira, podemos cancelar o x do numerador e do denominador da fração:
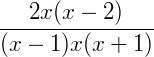
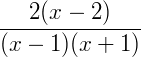
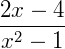
Exemplo 4) Agora, vamos ver se a expressão abaixo pode ser reduzida ou fatorada:
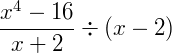
Como se trata de uma divisão de frações, podemos dizer que:
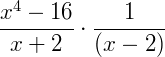
Fatorando a expressão do numerador temos:
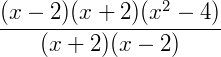
Concluindo então:
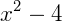
Referências Bibliográficas:
GONÇALVES, Adilson. Introdução à Álgebra. Rio de Janeiro: IMPA, 1999.
MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.
Texto originalmente publicado em https://www.infoescola.com/matematica/fracoes-algebricas/