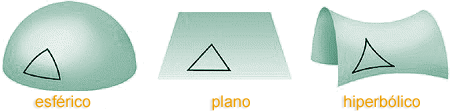
A Geometria Esférica foi elaborada a fim de ser possível o estudo geométrico em áreas esféricas, onde a Geometria Euclidiana não consegue ser usada de forma precisa.
Esta por sua vez é usada para estudarmos os aspectos da superfície plana e não conseguimos usá-la para o estudo de superfícies esféricas. Um exemplo que comprova isso: desenhe uma figura qualquer em uma folha de papel, um quadrado ou um triângulo. Em seguida recorte essa figura e tente colocá-la recobrindo uma bolinha de isopor ou qualquer outro objeto esférico; não será possível apoiar toda a área do recorte feito, pois as propriedades das superfícies planas são diferentes das propriedades da superfície esférica, tal razão foi a motivação para a elaboração da Geometria Esférica. Uma outra diferença entre a Geometria Euclidiana e a Geometria Esférica, é o fato da primeira ter os seus conceitos básicos baseados em linhas e eixo cartesiano; já a segunda é baseada em Geodésicas e ângulos. Geodésicas são os menores segmentos possíveis que unem dois pontos de uma superfície, e no caso de uma esfera, as suas Geodésicas serão segmentos curivilíneos medidos ao longo do arco de circunferência máxima da esfera.
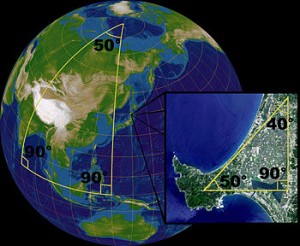Existem várias características curiosas quanto a Geometria Esférica e para explicá-las o leitor deverá ter em mente que estamos, obviamente, trabalhando com superfícies esféricas e não planas, a qual estamos habituados. A primeira delas é que é impossível desenharmos duas figuras com exatamente a mesma forma mas com tamanhos diferentes. Este efeito acontece porque neste tipo de geometria o tamanho da figura desenhada influencia na sua forma (e a forma da figura influencia em seu tamanho); se desejarmos figuras com a mesma forma e tamanhos diferentes, devemos desenhar cada uma delas em esferas de tamanhos diferentes. Uma segunda característica é o fato de não existirem segmentos que sejam paralelos, todos eles se cortam em algum ponto da superfície. Uma terceira característca importante é a soma dos ângulos internos de um triângulo que esteja desenhado sobre uma esfera, ela sempre excede 180 graus. Na figura ao lado temos um exemplo de um triângulo com a soma dos ângulos internos maior que 180 graus.
A Geometria Esférica começou a ser estudada pelos matemáticos no século XIX, mas eles eram duramente repreendidos por seus colegas. Mas estes matemáticos não se acovardaram cientificamente e finalizaram seus estudos. Hoje em dia a Geometria Esférica é de grande valor na navegação e astronomia.
Fontes:
http://pt.wikipedia.org/wiki/Geometria_esf%C3%A9rica
http://www.atractor.pt/simetria/matematica/docs/triangulos3.htm
http://www.slideshare.net/paulocaratsoris/geometria-nao-euclidiana
http://www.miniweb.com.br/ciencias/artigos/a_geometria_dos_espacos_curvos.pdf
Ilustração: http://www.cepa.if.usp.br/e-fisica/mecanica/universitario/cap03/cap3_04.php
Texto originalmente publicado em https://www.infoescola.com/matematica/geometria-esferica/