Mínimo Múltiplo Comum (MMC)

Operação de minimização

Consideremos os conjuntos do múltiplos de 6, 9 e 12:

M(6) = {0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, ...}

M(9) = {0, 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, ...}

M(12) = {0, 12, 24, 36, 48, 60, 72, 84, 96, ...}

Os múltiplos comuns de 6, 9 e 12 são os elementos do conjunto

M(6) ∩ M(9) ∩ M(12) = {0, 36, 72, 108, ...} = M(36)

O menor desses múltiplos comuns diferentes de zero (no caso, 36) é chamado mínimo múltiplo comum de 6, 9 e 12. Escrevemos:

M.M.C. (6, 9, 12) = 36

que é um conjunto infinito, ordenado, mas sempre possui um mínimo, isto é, um valor menor que todos os outros.

Podemos definir, portanto:

Dados dois ou mais números naturais, chama-se Mínimo Múltiplo Comum desses números o menor número natural não nulo que é múltiplo ao mesmo tempo de todos eles.

Cálculo do MMC de vários números

1º Processo: decomposição em fatores primos

Vejamos, de início, o que deve ocorrer entre os fatores primos de um número N e de um seu múltiplo M.

36 = 2² x 3²
e
9 = 3²

Isto é, 36 contém 3² ou 3 x 3, que são os fatores primos de 9.

Outro exemplo:

180 é múltiplo de 45. Vê-se que:

180 = 2² x 3³ x 5
e
45 = 3² x 5.

Ou seja, 180 contém todos os fatores primos de 45.

Podemos dizer que:

Se M é múltiplo de N, então, M contém todos os fatores primos de N

Calculemos, a seguir, o M.M.C. (12, 30, 42).

Feita a decomposição, obtemos:

12 = 2² x 3

30 = 2 x 3 x 5

42 = 2 x 3 x 7

Ora, para que um número M seja múltiplo de 12, 30 e 42, deve conter, pelo menos, todos os fatores primos que aparecem em 12, 30 e 42. Assim, deve conter os fatores:

2² x 3 x 5 x 7, pelo menos.

Se possuir apenas esses fatores será o menor múltiplo comum ou mínimo múltiplo comum dos números dados.

Conclui-se, então, a seguinte regra:

a) Decompõem-se os números em fatores primos.

b) Toma-se o produto dos fatores primos comuns e não comuns a essas decomposições, cada um deles tomado com o maior dos expoentes que esse fator possui nas decomposições.

Exemplo:

Calcular o M.M.C. (105, 625, 343)

Decompondo-se, temos:

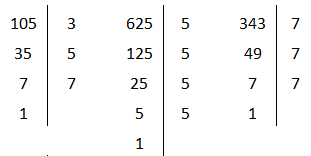
105 = 3 x 5 x 7

625 = 5⁴

343 = 7³

M.M.C. (105, 625, 343) = 3 x 5⁴ x 7³ = 643.125

2º Processo: fatoração simultânea

1º) Identificamos o menor número primo que divide pelo menos um dos números dados. No caso, o menor primo é 2. Efetuamos as divisões (quando exatas) ou repetimos o número (quando a divisão não é exata).

2º) Continuamos a divisão pelo mesmo número 2, enquanto houver pelo menos uma divisão exata.

3º) Não havendo agora, na última linha, nenhum número divisível por 2, procuramos o próximo número primo que divide pelo menos um deles. É claro que é 3. Continuamos com esse procedimento até que na última linha só apareça o número 1.

4º) O produto dos números primos à direita do traço vertical é o M.M.C. dos números dados.

Exemplo:

Seja, então, calcular o M.M.C. (360, 150, 45).

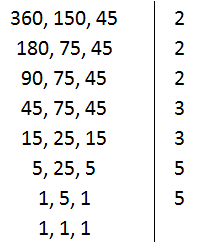
Após a decomposição simultânea, basta multiplicar os fatores primos:

M.M.C. (360, 150, 45) = 2³ x 3² x 52 = 1800

Exercícios resolvidos

1º) (UTF-PR) Três vendedores viajam a serviço para uma empresa. O primeiro viaja de 12 em 12 dias, o segundo de 16 em 16 dias e o terceiro de 20 em 20 dias. Se todos viajarem hoje, calcule daqui quantos dias eles voltarão a viajar no mesmo dia.

A) 220 dias
B) 120 dias
C) 240 dias
D) 250 dias
E) 180 dias

Resolução:

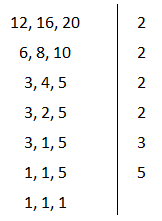
O dia da próxima viagem simultânea dos três vendedores deve ser igual ao mínimo múltiplo comum da duração de cada viagem. Assim, temos que M.M.C. (12, 16, 20) = 2⁴ x 3 x 5 = 240 dias.

Resposta: letra C.

2º) (FUVEST) No alto de uma torre de uma emissora de televisão, duas luzes piscam com frequências diferentes. A primeira pisca 15 vezes por minuto e a segunda pisca 10 vezes por minuto. Se num certo instante luzes piscam simultaneamente, após quantos segundos elas voltarão a piscar simultaneamente?

A) 12
B) 10
C) 20
D) 15
E) 30

Resolução:

O tempo, em segundos, em que as luzes piscarão juntas simultaneamente deve ser igual ao mínimo múltiplo dos tempos 15 segundos e 10 segundos. Assim, temos que M.M.C. (10, 15) = 2 x 3 x 5 = 30 dias.

Resposta: letra E

3º) Em um terminal rodoviário, sabe-se que:

• A cada 50 minutos parte um ônibus da linha Amarela;
• A cada 30 minutos parte um ônibus da linha Verde;
• A cada 40 minutos parte um ônibus da linha Branca.

Considerando-se que às 8h houve uma partida simultânea de um ônibus de cada uma das três linhas, e considerando que o quadro de horários não sofrerá alterações, determinar a hora exata em que a próxima partida simultânea ocorrerá.

Resolução:

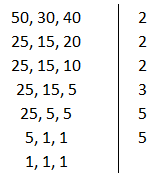
O tempo da próxima partida simultânea deve ser igual ao mínimo múltiplo comum dos tempos de partida de cada uma das linhas. Assim, temos que M.M.C. (50, 30, 40) = 2³ x 3 x 5² = 600 minutos = 10 horas. Portanto, a próxima partida simultânea ocorrerá às 8h + 10 h = 18 horas

Referências bibliográficas:

1. LIMA, Elon Lages; CARVALHO, Paulo C. P.; WAGNER, Eduardo; MORGADO, Augusto C. A Matemática do Ensino Médio. vol. 1. Coleção do Professor de Matemática, SBM, 2012.

2. MOREIRA, Carlos T. de A.; SALDANHA, Nicolau C.; MARTINEZ, Fábio E. B. Tópicos em Teoria dos Números, Coleção PROFMAT, 2012.

3. HEFEZ, Abramo. Elementos de Aritmética. Coleção Textos Universitários, SBM. Edição 2006.

Texto originalmente publicado em https://www.infoescola.com/matematica/minimo-multiplo-comum-mmc/