O princípio multiplicativo é a ferramenta básica utilizada para resolver problemas de contagem. Sua aplicação direta na resolução de problemas pode às vezes tornar-se trabalhosa. Percebemos, contudo, que alguns problemas possuem características em comum e são recorrentes. Iremos a seguir, definir o agrupamento chamado Permutação Simples.
Conteúdo deste artigo
O que é uma permutação simples?
Suponha que tenhamos 5 pessoas, A, B, C, D e E que vão posar para uma fotografia. De quantas maneiras elas podem ser dispostas numa fila lado a lado?
Algumas das possíveis filas que podem ser organizadas são: ABCDE, ABCED, ACBDE, ACDEB, etc. Cada uma delas é obtida por meio de uma permutação simples.
Permutação simples é qualquer agrupamento que se pode formar com todos os elementos disponíveis no problema, usando cada um deles uma única vez, e que se diferenciam um do outro apenas pela posição em que esses elementos aparecem no agrupamento.
Indica-se: 
Cálculo do número de permutações simples
Calcular o número de permutações simples de n elementos é o mesmo que calcular quantas são as ordenações possíveis dos n elementos de um conjunto.
Exemplo: Suponha que um conjunto tenha quatro elementos. Quantas são as ordenações possíveis para esses objetos?
Resolução:
- 1º) escolha do primeiro elemento: 4 possibilidades;
- 2º) escolha do segundo elemento: 3 possibilidades;
- 3º) escolha do terceiro elemento: 2 possibilidades;
- 4º) escolha do terceiro elemento: 1 possibilidade.
Aplicando o princípio fundamental da contagem (PFC), temos: 4 x 3 x 2 x 1 = 24 ordenações diferentes. Dizemos que  (o número de permutações de quatro elementos é 24)
(o número de permutações de quatro elementos é 24)
Generalizando
Caso nosso conjunto tenha n elementos, um raciocínio semelhante ao anterior nos permite dizer que teremos n . (n -1) . (n -2) . (n – 3) ... 3 . 2 . 1 ordenações. Esse produto é chamado fatorial do número natural n e é representado por n!
Se um conjunto possui n elementos, ele terá  permutações simples.
permutações simples.

Exercícios resolvidos
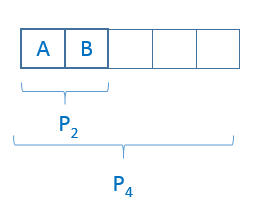
1º) De quantas maneiras diferentes podemos arrumar 5 livros em uma estante, de maneira que 2 permaneçam sempre juntos?
Consideremos A e B os dois livros que deverão permanecer juntos. Nesse caso, vamos considerar que A e B constituem uma única posição. Permutando essas quatro posições, encontramos todas as sequências possíveis. Como A e B podem ser ordenados de P2 modos diferentes, a resposta será:
P2 . P2 = 2 . 4! = 2 . 24 = 48
2º) Formados e colocados em ordem crescente todos os números de 4 algarismos obtidos com os algarismos 1, 3, 5 e 7 (sem repetir), que lugar ocupa o número 5731?
Resolução:
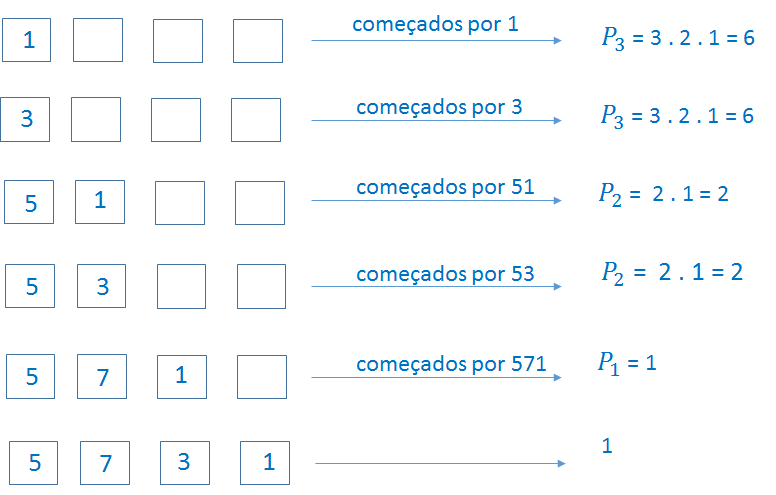
Logo, existem 6 + 6 + 2 + 2 + 1 = 17 números menores, portanto, sua posição é a 18ª.
3º) Num tribunal, dez réus devem ser julgados isoladamente num mesmo dia; três são paulistas, dois mineiros, três gaúchos e dois baianos. Determine o número de formas de não se julgar consecutivamente três paulistas.
Resolução:
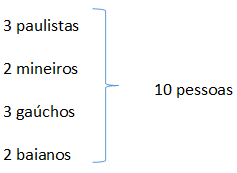
Para se julgar 3 pessoas paulistas pode ser calculado como: 
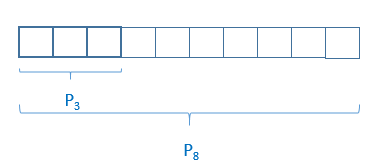
Logo, o resultado final é:

4º) Numa van viajam 9 pessoas, das quais 4 podem dirigir. De quantas maneiras diferentes é possível acomodá-las na van ( 3 bancos na frente, 3 no banco do meio e 3 no banco traseiro) de forma que uma das 4 que dirigem ocupe o lugar da direção?
Resolução:
Para cada pessoa que dirige, as oito restantes podem se acomodar de 8! maneiras. Como são 4 pessoas que dirigem, temos:
Número de maneiras ⇒ 4 . 8! = 4 x 40320 = 161280
Referências bibliográficas:
1. MORGADO, Augusto C.; CARVALHO, João B. P. de; CARVALHO, Paulo Cezar P.; FERNANDEZ, Pedro – Análise Combinatória e Probabilidade – 9ª ed. – Rio de Janeiro, SBM, 1991
2. SANTOS, José Plínio O.; MELL, Margarida P.; MURARI, Idani T. C. – Introdução à Análise Combinatória – 4ª edição revista – Rio de Janeiro: Editora Ciência Moderna, 2007.
3. LIMA, Elon Lages. A Matemática do Ensino Médio. Volume 2, 6.ed. Coleção do Professor de Matemática. Rio de Janeiro: SBM, 2006.
Texto originalmente publicado em https://www.infoescola.com/matematica/permutacao/