Porcentagem

A porcentagem é uma das áreas da matemática mais conhecidas. Praticamente é utilizada em todas as áreas, quando queremos comparar grandezas, estimar o crescimento de algo, expressar uma quantidade de aumento ou desconto do preço de alguma mercadoria. Vemos porcentagem a todo momento e, mesmo quando não percebemos, estamos fazendo uso dela.

A porcentagem é uma razão cujo o denominador é igual a 100.

$\frac{k}{100}$

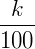
Porcentagens são chamadas, também de razão centesimal ou de percentual.

As porcentagens costumam ser indicadas pelo símbolo “%”, lê-se “por cento”.

Podemos representar uma fração na forma fracionária, decimal, ou acompanhada do símbolo %. Veja:

$4\% = \frac{4}{100} = 0,04$

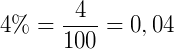
As porcentagens podem ser utilizadas quando queremos expressar que uma quantidade é uma parte de outra, por exemplo, imagine que um produto que custava R$ 80,00 foi vendido a vista, com 5% de desconto. Esse desconto de 5% de R$ 80,00 significa 5 partes das 100 em que 80 foi dividido, ou seja, R$ 80,00 será dividido em 100 partes, e o desconto será igual a 5 partes dessa divisão. Assim,

5% de R$ 80,00 = 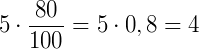$5 \cdot \frac{80}{100} = 5 \cdot 0,8 = 4$

Portanto, 5% de R$ 80,00 será R$ 4,00. E esse será o valor a ser descontado.

Poderíamos, também, calcular de outra forma:

5% de R$ 80,00 = 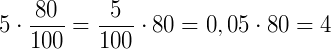$5 \cdot \frac{80}{100} = \frac{5}{100} \cdot 80 = 0,05 \cdot 80 = 4$

Daí, concluímos que calcular a% de x, corresponde a fazer:

$\frac{a}{100} \cdot x$

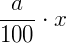
Podemos usar, também, a seguinte proporção:

$\begin{cases}100\% &\longrightarrow 80 \\ 5\% &\longrightarrow x\end{cases}$

$100x = 80 \cdot 5$

$100x = 400$

$x = \frac{400}{100}$

$x = R\$\text{ 4}$

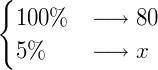
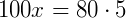
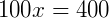
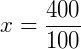
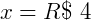
Exemplo

(ENEM 2013). Para aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.

Um cliente deseja comprar um produto que custava R$50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja. Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de

1. 15,00
2. 14,00
3. 10,00
4. 5,00
5. 4,00

O primeiro desconto será de 20% sobre o produto que custa R$ 50,00.

20% de R$ 50 = 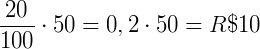$\frac{20}{100} \cdot 50 = 0,2 \cdot 50 = R\$ 10$

Assim, o cliente terá um desconto de R$ 10,00. O cliente pagará, então R$ 40,00.

Se o cliente tivesse o cartão fidelidade, ainda receberia um desconto adicional de 10% sobre o valor de R$ 40,00 (após o desconto de 20%).

O desconto será 10% de 40 = 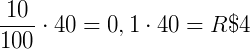$\frac{10}{100} \cdot 40 = 0,1 \cdot 40 = R\$ 4$. Ou seja, o desconto seria de R$ 4,00. O cliente pagaria, então R$ 36,00.

A economia adicional será a diferença entre os preços pagos com o cartão fidelidade e sem ele, ou seja, R$ 40,00 – R$ 36,00 = R$ 4,00.

Alternativa "e"

Referências:

DANTE, Luiz Roberto. Matemática: contexto & aplicações. 3. ed. São Paulo: Ática, 2013.

DEGENSZAJN, David; HAZZAN, Samuel. IEZZI, Gelson. Fundamentos de Matemática Elementar. Matemática Comercial, Matemática Financeira, Estatística Descritiva. Vol. 11. São Paulo: Atual, 2004.

Texto originalmente publicado em https://www.infoescola.com/matematica/porcentagem/