Há dois tipos de fenômenos que são objeto de estudo científico: os fenômenos determinísticos e os fenômenos aleatórios.
Em um experimento determinístico, os resultados possíveis são previsíveis antecipadamente. Conhecemos as leis que os governam a ponto de afirmarmos que que tais experimentos, repetidos nas mesmas condições, apresentam sempre os mesmos resultados. Podemos citar, como exemplo, a queda livre, que é um movimento no qual os corpos quando abandonados de certa altura são acelerados pela força da gravidade em direção ao solo.
Já em um fenômeno aleatório, os experimentos correspondentes, repetidos nas mesmas condições, não necessariamente produzem os mesmos resultados. Apesar de não conseguirmos prever antecipadamente qual resultado será obtido, em geral, somos capazes de descrever o conjunto de todos os resultados possíveis para esses experimentos.
Conteúdo deste artigo
- Conceitos básicos
- O que os experimentos acima têm em comum?
- Experimento aleatório
- Espaço amostral
- Evento
- União e interseção de eventos
- Eventos complementares
- Eventos independentes e eventos dependentes
- Eventos com reposição e eventos sem reposição
- Definição clássica para probabilidade
- Exercícios resolvidos
- Probabilidade condicional
- Exercícios resolvidos
- Probabilidade de eventos independentes
- Exercícios e questões de vestibulares
Conceitos básicos
Vamos começar apresentando alguns experimentos:
- Jogue um dado e observe o número mostrado na face de cima.
- Jogue uma moeda quatro vezes e observe o número de caras obtido.
- Lance um dado e observe sua face voltada para cima.
- Sortear uma carta de um baralho e observar seu naipe.
- Jogue uma moeda quatro vezes e observe a sequência obtida de caras e coroas.
- Em uma linha de produção, fabrique peças em série e conte o número de peças defeituosas produzidas em um período de 24 horas.
- Um lote de 10 peças contém 3 defeituosas. As peças são retiradas uma a uma (sem reposição da peça retirada) até que a última peça defeituosa seja encontrada. O número total de peças retiradas do lote é contado.
- Peças são fabricadas até que 10 peças perfeitas sejam produzidas. O número total de peças fabricadas é contado.
O que os experimentos acima têm em comum?
- Cada experimento poderá ser repetido indefinidamente sob condições essencialmente inalterados.
- Embora não sejamos capazes de prever antecipadamente qual resultado particular ocorrerá, seremos capazes de descrever o conjunto de todos os possíveis resultados do experimento.
Experimento aleatório
É qualquer experimento cujo resultado não se consegue prever.
Ainda que repetido em condições iguais ou muito semelhantes, um mesmo experimento aleatório pode apresentar resultados diferentes.
Espaço amostral
Espaço amostral é o conjunto de todos os resultados possíveis de um experimento aleatório.
Em geral utilizamos a letra grega maiúscula Ω (lê-se ômega) para representar o espaço amostral de um experimento aleatório.
1. Lançamento de uma moeda
Ω = {cara, coroa} = {c, k}
2. Lançamento de um dado (cubo)
Ω = {1, 2, 3, 4, 5, 6}
3. Sorteio de uma carta de baralho
Ω = {copas, paus, ouros, espadas}
Evento
Evento é um subconjunto qualquer do espaço amostral.
Exemplo:
Uma urna contém 10 bolas numeradas de 1 a 10. Retira-se uma bola ao acaso e se observa o número indicado. Descrever os seguintes conjuntos:
- O espaço amostral Ω.
- O evento A: o número da bola é ímpar.
- O evento B: o número da bola é múltiplo de 3.
Solução:
- Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
- A = {1, 3, 5, 7, 9}
- B = {3, 6, 9}
União e interseção de eventos
A união de dois eventos A e B, denotada por A ∪ B, representa a ocorrência de pelo menos um dos eventos A ou B.
A interseção do evento A com B, denotada por A ∩ B, é a ocorrência simultânea de A e B.
Dois eventos A e B são disjuntos ou mutuamente exclusivos quando não tem elementos em comum. Isto é, A ∩ B = Ø.
Exemplo:
Em uma cidade onde se publicaram três jornais, A, B e C, constatou-se que, entre 1.000 famílias, assinam A: 470; B: 420; C: 315; A e B: 110; A e C: 220; B e C: 140; e 75 assinam os três. Escolhendo-se ao acaso uma família, qual a probabilidade de que ela:
- A) não assine nenhum dos três jornais?
- B) assine apenas um dos três jornais?
- C) assine pelo menos dois jornais?
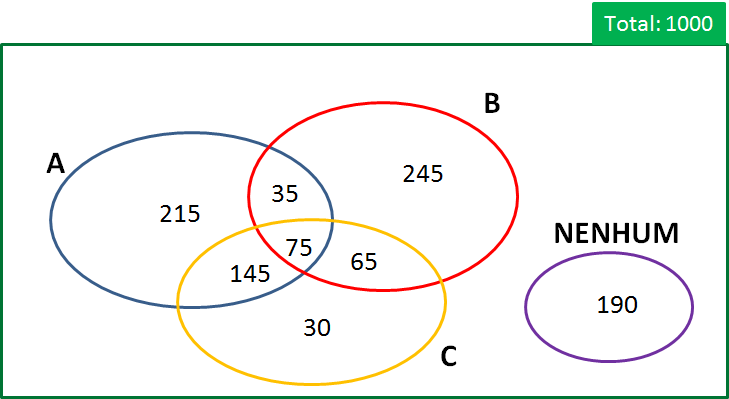
Solução:
De acordo com o diagrama ao lado, temos:
a) 190 famílias → 190/1000 = 19% de probabilidade
b) 215 + 245 + 30 = 490 → 490/1000 = 49% de probabilidade
c) 145 + 35 + 65 + 75 = 320 → 320/1000 = 32% de probabilidade
Eventos complementares
Dizemos que A e B são complementares se sua união é o espaço amostral e sua interseção é vazia. O complementar de A será representado por AC e temos A ∪ AC = Ω e A ∩ AC = Ø.
Exemplo:
Em certo teste da loteria esportiva, temos que a probabilidade de ocorrer a coluna 1 é de 39% e de ocorrer a coluna 3 é 23%. Calcular a probabilidade de, nesse mesmo jogo, ocorrer a coluna 2, sabendo que só há 3 colunas.
Resolução:
O experimento consiste em três eventos:
- A: ocorrer a coluna1;
- B: ocorrer a coluna 2;
- C: ocorrer a coluna 3.
Temos que P(A) + P(B) + P(C) = 100%
Logo: 39% + P(B) + 23% = 100%
P(B) = 100% - 62% = 38%
Eventos independentes e eventos dependentes
Dois eventos são independentes quando a ocorrência ou a não ocorrência de um evento não tem efeito algum na probabilidade de ocorrência do outro evento.
Dois eventos são dependentes quando a ocorrência ou não ocorrência de um evento afeta a probabilidade de ocorrência do outro evento.
Eventos com reposição e eventos sem reposição
Com reposição significa o retorno do evento sorteado ao seu conjunto de origem. É isso que mantém a probabilidade de sorteio constante, portanto, não se altera a probabilidade de sorteio de evento seguinte.
Sem reposição significa o não retorno do evento sorteado ou do seu conjunto de origem, alterando a probabilidade de sorteio do evento.
Definição clássica para probabilidade
Quando todos os elementos do espaço amostral têm a mesma probabilidade de ocorrer, a definição clássica de probabilidade e um evento A ocorrer é dada por:

Exercícios resolvidos
1) Qual a probabilidade de, ao lançarmos um dado, obtermos o número 2?
Resolução:
O espaço amostral é S={1,2,3,4,5,6}
Logo, o número de casos possíveis é 6. Já o evento considerado é formado apenas pelo número 2, ou seja, E={2}, então, o número de casos favoráveis é 1.
Portanto:
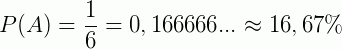
Probabilidade condicional
Se a probabilidade de ocorrência de um evento B interfere na probabilidade de ocorrência de um evento A, então dizemos que a probabilidade de A está condicionada à probabilidade de B e representamos por P(A/B). Lê-se: probabilidade de A dado B.
A/B significa a ocorrência do evento A sabendo que o evento B já ocorreu ou que a ocorrência de B esteja garantida (os eventos A e B são dependentes).
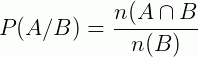
Exercícios resolvidos
1) Foi feita uma pesquisa de mercado sobre o uso de dois perfumes cujas marcas representaremos por A e B.O quadro a seguir mostra os resultados dessa pesquisa, indicando quantos homens (M) e quantas mulheres (F) usam cada perfume.
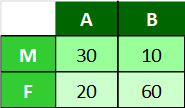
A) Qual probabilidade a escolhendo-se uma dessas pessoas ao acaso, ela ser usuário do perfume B?
B) Escolhendo-se uma dessas pessoas ao acaso, qual a probabilidade de ela ser mulher, sabendo-se que se trata de uma usuária do perfume A?
C) Qual a probabilidade de essa pessoa ser usuária do perfume A, sabendo-se que é uma mulher?
Resolução:
A) Temos, no total, 120 pessoas e, dessas pessoas, 70 são usuárias do perfume B. Logo 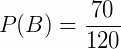 ou
ou 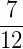 .
.
B) Queremos calcular P(F/A). Nosso novo espaço amostral reduzido é A, e ele tem 50 elementos. Nesse novo espaço, temos 20 mulheres. Logo: 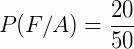 ou
ou  ou 40%.
ou 40%.
C) Queremos calcular P(A/F). O novo espaço amostral é F e tem 80 elementos. Nesse espaço o número de pessoas que usam o perfume A é 20. Portanto: 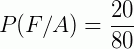 ou
ou  ou 25%.
ou 25%.
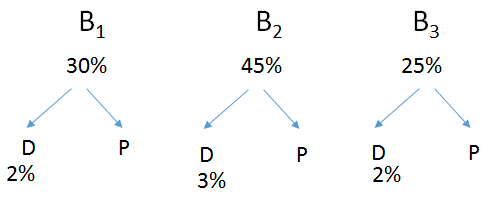
2) Em certa linha de montagem, três máquinas B1, B2 e B3 produzem 30%, 45% e 25% dos produtos, respectivamente. Sabe-se, de experiências anteriores, que 2%, 3% e 2% dos produtos feitos por cada máquina são, respectivamente, defeituosos. Agora, suponha que um produto, já acabado, seja selecionado aleatoriamente.
A) Qual a probabilidade do produto selecionado seja defeituoso?
B) Sabendo-se que o produto é defeituoso, qual é a probabilidade de que tal produto tenha sido fabricado pela máquina B1?
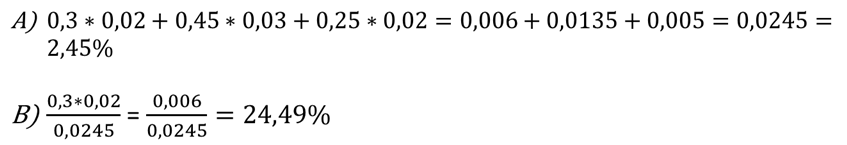
Probabilidade de eventos independentes
Dois eventos, A e B, são chamados independentes quando a probabilidade de ocorrência de um deles não interfere na probabilidade de ocorrência do outro, ou seja:
P(B/A) = P(B) ou P(A/B) = P(A)
Se A e B são eventos independentes, então a probabilidade de ocorrência de A e B será:
P(A ∩ B) = P(A) x P(B)
Exemplo: um grupo de pessoas é formado por 7 mulheres e 12 homens. Escolhe-se, ao acaso, duas dessas pessoas, uma após a outra. Calcular a probabilidade de:
A) A primeira pessoa ser uma mulher e a segunda um homem.
B) As duas pessoas serem homens.
Resolução:
A) Seja A o evento A={a primeira pessoa escolhida é mulher} e B={a segunda pessoa escolhida é homem}. Queremos calcular P(A ∩ B).
Como P(A ∩ B) = P(A) . P(A/B), temos P(A ∩ B) = 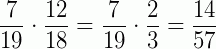 .
.
B) A probabilidade da primeira pessoa escolhida ser homem é 12/19. Já a probabilidade de a segunda pessoa escolhida ser homem, dado que a primeira foi homem, é 11/18. Logo, a resposta final será 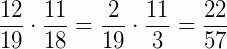 .
.
Texto originalmente publicado em https://www.infoescola.com/matematica/probabilidade/
