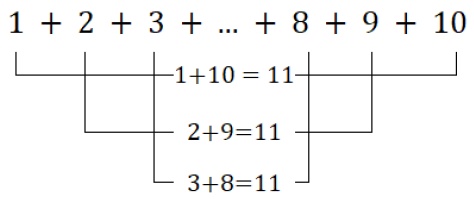O termo “progressão aritmética” remete a um desenvolvimento gradual de um processo ou uma sucessão. Em matemática, dizemos que esta sucessão é uma sequência. Podemos exemplificar algumas sequências conhecidas:
- Sequência das eleições para o Executivo a partir de 1994: (1994, 1998, 2002, 2006, 2010, 2014);
- Sequência das edições da Copa do Mundo a partir de 1990: (1990, 1994, ..., 2014, 2018);
- Sequência dos números naturais: (0, 1, 2, 3, 4, 5, ...)
Note que em todos os exemplos acima, as sequências são definidas por uma ordem em seus elementos (também chamados de termos). Definimos o tamanho de uma sequência pelo número de termos que ela possui, o que nos traz a possibilidade de que ela seja infinita ou finita.
Em uma sequência, finita ou infinita, nomeamos os termos em função de sua posição, ou seja, nos exemplos acima temos que o 1º termo de cada um são: 1994, 1990 e 0. O segundo termo: 1998, 1994 e 1. Assim, determinamos que um termo de uma sequência em função de sua posição pode ser chamado de , onde n representa a sua posição (1ª, 2ª, 3ª, ..., nª). Dizemos também que o primeiro e o último termo de uma sequência finita ( e ) são chamados de extremos de uma sequência. Podemos então representa-la de uma forma genérica:
(a1, a2, a3, a4, ... an)
Definição formal de Sequência Numérica
“Uma sequência numérica é uma função f, definida no conjunto dos números naturais, ou inteiros positivos tal que:
. Onde o n é chamado de índice e
o n-ésimo elemento da sequência, ou termo geral.”
Conteúdo deste artigo
Termo Geral de uma Progressão Aritmética
Perceba que, nos exemplos acima, todos os termos das sequências, a partir do 2º, são obtidos com a soma de um número fixo. Vejamos a sequência dos números naturais: Cada termo, iniciando com 0 (a1) é obtido somando 1 ao seu anterior. Ou seja:
a2 = a1 + 1 = 1
a3 = a2 + 1 = (a1+1)+1 = 2
a4 = a3 + 1 = (a2+1)+1 = [(a1+1)+1]+1 = 3
...
No caso da sequência dos números naturais, o número 1 que é somado a cada termo é chamado de razão da progressão (r). Em uma progressão aritmética (P.A.), cada termo de uma sequência é a soma do elemento anterior com sua razão. Se analisarmos os outros exemplos, vemos que elas possuem uma razão igual a 4. Vamos agora reescrever os termos da sequência em função de r (razão).
a2 = a1 + r
a3 = a2 + r = (a1+r)+r = a1+2r
a4 = a3 + r = (a2+r)+r = [(a1+r)+r]+r = a1+3r
...
Ora, se continuarmos realizando esta operação para os próximos termos, encontramos então uma fórmula para determinar o termo geral de uma progressão aritmética, que será dado por:
an = a1 + (n-1)r
E supondo um caso em que não sabemos qual é o seu primeiro termo, podemos usar uma forma generalizada do termo geral da P.A. Sejam m e n posições quaisquer dos termos, temos:
an = am + (n-m)r
Imagine que nosso desejo seja obter o 500º termo da sequência dos números naturais. Como a1 = 0, r = 1 e buscamos o termo a500, pela fórmula teremos:
a500 = a1+(500-1)r
a500 = 0+(500-1) . 1
a500 = 499
O termo da 500ª posição dos números naturais é o número 499.
Propriedade importante!
Qualquer termo de uma P.A., a partir do segundo termo (a2), é sempre igual à média aritmética entre os termos anterior e posterior a ele. Então para n ≥ 2, temos que:

Exemplo: Seja a sequência em progressão aritmética definida por (-7, -2, 3, 8, 13, 18), note que:


Soma dos termos de uma progressão aritmética finita
Tomemos a sequência dos números naturais de 1 a 10: (1, 2, 3, 4, ..., 8, 9, 10) e representaremos a soma de 10 termos da P.A. por S10. Então escrevemos:
S10 = 1 + 2 + 3 + ... + 8 + 9 + 10
O matemático Carl Friedrich Gauss (1777-1855) notou que em toda PA finita existe uma relação em que ao escolhermos um termo qualquer em uma sequência e somarmos ao seu extremo simétrico (ou o seu termo equidistante) obtemos sempre o mesmo valor, veja abaixo:
Gauss utilizou este procedimento para obter a fórmula da soma dos termos da PA. No exemplo acima, notem que teremos, no total, n/2 parcelas de valor (n+1), ou seja (5 x 11 = 55). Esta relação vale para a soma dos termos de uma P.A. Gauss constatou então que:
Sn = a1 + a2 + a3 + a4 + a5 + ... + an-2 + an-1 + an
Sn = (a1+an) + (a1+an) + ... + (a1+an)
Como existem n/2 parcelas iguais a (a1+an), então a fórmula é dada por:

Esta fórmula serve para qualquer PA de qualquer razão, pois independente do valor dos seus termos as propriedades das somas de suas parcelas também são válidas.
Referências Bibliográficas:
DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.
ÁVILA, Geraldo. Introdução à Análise Matemática. São Paulo: Blucher, 1999.
Texto originalmente publicado em https://www.infoescola.com/matematica/progressao-aritmetica/