Teorema de Pitágoras

O Teorema de Pitágoras é um dos assuntos mais conhecidos da Matemática. Ele é uma das primeiras coisas que lembramos quando falamos sobre geometria ou trigonometria. Sua descoberta foi importante para a época, pois impulsionou inúmeros outros estudos, os quais fizeram com que a matemática avançasse até os dias atuais. Seu enunciado é simples, assim como os cálculos envolvidos.

Esse teorema só pode ser aplicado em um triângulo retângulo, que é aquele onde há um ângulo igual a 90°, que chamamos de ângulo reto. Daí o nome, triângulo retângulo. Para compreender, veja, abaixo, uma figura.

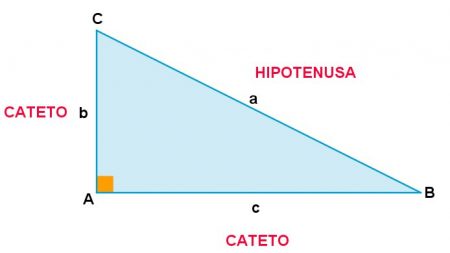
Em um triângulo retângulo, o lado maior, CB, recebe o nome de Hipotenusa. Este lado sempre estará oposto ao ângulo reto. Os outros dois lados, AC e AB recebem o nome de Cateto.

O enunciado do Teorema diz o seguinte:

“O quadrado da medida da hipotenusa é igual a soma do quadrado das medidas dos catetos”

Observando a figura acima, podemos resumir, matematicamente, o enunciado em:

$CB^2 = AB^2 + AC^2$

$a^2 = b^2 + c^2$

Demonstração

Existem muitas demonstrações para o Teorema de Pitágoras. Aqui, vamos explorar uma demonstração que toma como base as relações métricas num triângulo retângulo:

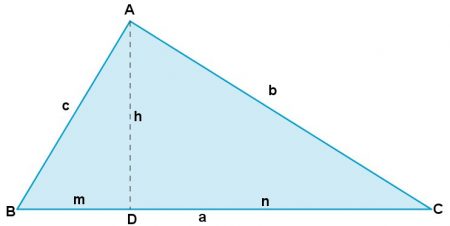
Considerando que o triângulo ABC é congruente ao triângulo DAC, temos a seguinte relação:

$\frac{a}{b} = \frac{b}{n} \Rightarrow b^2 = a \cdot n$

Considerando que o triângulo ABC é congruente ao triângulo DBA, temos a seguinte relação:

$\frac{a}{c} = \frac{c}{m} \Rightarrow c^2 = a \cdot m$

Agora vamos somam, membro a membro essas duas equações:

$b^2 = a \cdot n$

$c^2 = a \cdot m$

$b^2 + c^2 = an + am$

$b^2 + c^2 = a(n+m)$

Observe que n + m = a, assim:

$b^2 + c^2 = a(n+m)$

$b^2 + c^2 = a \cdot a$

$b^2 + c^2 = a^2$

Exemplo:

(ENEM). Na figura abaixo, que representa o projeto de uma escada de 5 degraus de mesma altura, o comprimento total do corrimão é igual a:

• A) 1,8 m.
• B) 1,9 m.
• C) 2,0 m.
• D) 2,1 m
• E) 2,2 m.

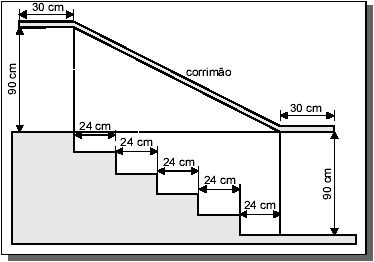
Observe que a altura entre o primeiro degrau e o corrimão é de 90 cm. Somando o comprimento de cada degrau, obteremos 5 . 24 = 120 cm

Observe que será formado um triângulo retângulo de catetos 90 cm e 120 cm. Podemos aplicar o Teorema de Pitágoras para encontrar a medida do corrimão:

$a^2 = b^2 + c^2$

$a^2 = 90^2 + 120^2$

$a^2 = 8100 + 14400$

$a^2 = 22500$

$a = \sqrt{22500}$

$a = 150 cm$

Assim, o corrimão terá 150 cm. Mas observe que ainda há dois pedaços do corrimão, ambos de 30 cm, assim, a medida do corrimão será 150 cm + 60 cm = 210 cm. Transformando para metros (dividindo por 100) teremos 2,1 m. Alternativa D.

Referência:

DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.

Texto originalmente publicado em https://www.infoescola.com/matematica/teorema-de-pitagoras/