O estudo dos conteúdos matemáticos, bem como suas aplicações, é necessário para que se tenha uma visão de mundo mais límpida e coerente com os aspectos de uma sociedade complexa e metamórfica. Compreender os porquês e os pra quês do que se estuda, possibilita ao aprendiz a independência cognitiva e o domínio integral do saber. Nesse artigo, abordar-se-á alguns conceitos e aplicações da unidade de medida de comprimento, o metro, seus múltiplos e submúltiplos, assim como, os aspectos históricos, as necessidades de adoção de um sistema de base decimal unificado e todo um enredo que envolve matemática e cotidiano.
Aspectos Históricos
Desde tempos pretéritos que há a necessidade de um consenso no que se refere à padronização dos sistemas de medidas. Diante da diversidade de medidas e medidores a sociedade viu-se atingida por métodos arbitrários causadores de prejuízos e injustiças nos mais diversos aspectos. Um dos meios usados para medir tinha como ferramenta medidora partes do corpo como: mão (palmo), dedo (polegada), braço (braça e côvado), etc. Como havia variância de tamanho dos elementos citados anteriormente, jamais existiam medidas precisas, resultando em números arbitrários e causadores de “controvérsias matemáticas”.
No ano 1789 foi feito um pedido pelo Rei da França aos membros da Academia de Ciências daquela nação para que formulassem um sistema de medidas unificado. Assim, entrou em vigor naquele país o sistema de medidas de base decimal com três unidades titulares: o metro, para medir o comprimento, o litro, para medir a capacidade e o quilograma, para medir a massa. No ano 1960 o sistema francês foi adotado mundialmente como Sistema Internacional de Medidas (SI). O novo sistema passou a ser utilizado por quase todos os países do mundo, com exceção de alguns, por sua praticidade e pela linguagem universal. No Brasil o SI tornou-se obrigatório no ano de 1962.
O metro, seus múltiplos e submúltiplos
O metro é utilizado cotidianamente em várias atividades humanas. Dele, deriva outras unidades das quais convencionou-se chamar de múltiplos – quando estas são resultados de uma multiplicação decimal a partir do metro, e de submúltiplos – quando forem resultados de uma divisão decimal.
| METRO (m) | |||||
| MÚLTIPLOS | SUBMÚLTIPLOS | ||||
| Unidade | Sigla | Relação | Unidade | Sigla | Relação |
| Decâmetro | dam | m x 10 | Decímetro | dm | m/10 |
| Hectômetro | hm | m x 100 | Centímetro | cm | m/100 |
| Quilômetro | km | m x 1000 | Milímetro | mm | m/1000 |
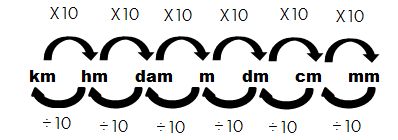
Outro mecanismo prático para fazer a conversão das unidades de medidas segue abaixo:
Para solucionar problemas contendo as unidades de medidas expostas nas tabelas acima, deve-se fazer a observação do posicionamento da unidade em conversão em relação à unidade fixa. Observe os exemplos a seguir:
- Converter a medida em metro (m): 2,5 km
1º Passo:
Observa-se a distância (número de casas decimais) da unidade km à unidade m, que nesse caso são 3 casas.
2º Passo:
Como m está à direita de km, escrevemos 2,5 x 1000 (resultado da multiplicação de 10 x 10 x 10, ou seja, a distância entre km e m).
3º Passo:
Em 2,5 “deslocamos a vírgula” três vezes para a direita (número de zeros de mil) e os espaços em branco preenchemos com zeros.
25/ 0 / 0, 0 = 2500,0 m, ou seja, 2,5 km = 2500 m.
- Converter a medida em quilômetros (km): 15 m
1º Passo:
Observa-se a distância (número de casas decimais) da unidade m à unidade km, que nesse caso são 3 casas.
2º Passo:
Como km está à esquerda de m, escrevemos 15 ÷ 1000 (resultado da multiplicação 10 x 10 x 10, ou seja, a distância entre m e km).
3º Passo:
Em 15 “deslocamos a vírgula” três vezes para a esquerda (número de zeros de mil) e os espaços em branco preenchemos com zeros.
0 ,0 /1/5 = 0,015 km, ou seja, 15m = 0,015 km.
Observação: lembre-se que o número 15 é o mesmo que 15,0.
Através do conhecimento dos números decimais e usando a técnica do “deslocamento da vírgula” pode-se sempre chegar aos resultados das conversões sem muito esforço e com muita facilidade. Para isso, basta seguir os passos das instruções anteriores ou desenvolver cálculos semelhantes baseados na observação dos números e suas propriedades.
Um pedreiro, ao ler as informações contidas em uma caixa de piso, que tinha suas pedras na forma quadrada, observou que cada pedra media 1600 cm2 de área, ou seja, 40 cm de lado. Para realizar a pavimentação de um cômodo residencial ele precisa de pedras quadradas com 20 cm de lado. Quantas pedras do tamanho desejado (20 cm de lado) ele poderá fazer com cada uma inteira (40 cm de lado)? Ao final, mostre a medida dos lados dessas pedras em metro (m).
Primeira solução:
- 1º Passo:
Observa-se os dados do problema em questão.
- Pedra inteira – 40 cm de lado; área de 1600 cm2;
- Pedra desejada – 20 cm de lado cada.
- 2º Passo:
Devemos encontrar a área das pedras desejadas pelo pedreiro, isto é, se elas são quadradas e possuem lados de 20 cm, basta que façamos:
A = 20 cm x 20 cm = 400 cm2
- 3º Passo:
Para encontramos a solução do primeiro problema basta que dividamos a primeira área (A1) pela segunda área (A2).
S = A1/A2
S = 1600 cm2 : 400 cm2
S = 4
Portanto, a partir das pedras originais cuja medida dos lados é de 40 cm, o pedreiro poderá fazer 4 pedras com medidas dos lados 20 cm.
Segunda solução:
- 1º Passo:
Pretende-se aqui mostrar as medidas dos lados, tanto das pedras originais quanto das pedras desejadas pelo pedreiro, em metro. O procedimento é simples, basta apenas seguir o modelo das transformações anteriores.
Converter as medidas 40 cm e 20 cm em metro (m):
2º Passo:
Observa-se a distância (número de casas decimais) da unidade cm à unidade m, que nesse caso são 2 casas.
3º Passo:
Como m está à esquerda de cm, escrevemos 40 ÷ 100 e 20 ÷ 100 (resultado da multiplicação 10 x 10, ou seja, a distância entre cm e m).
4º Passo:
Em 40, e em 20, “deslocamos a vírgula” duas vezes para a esquerda (número de zeros de cem) e os espaços vazios preenchemos com zeros.
0 ,4 / 0 = 0,40 ou 0,4 m, ou seja, 40 cm = 0,4 m.
0 , 2 / 0 = 0,20 ou 0,2 m, ou seja, 20 cm = 0,2 m.
Lembrete: Jamais se opera com unidades diferentes. Temos que converter as unidades a fim de efetuarmos cálculos precisos e matematicamente corretos.
Conclusão
Sabendo operar com o metro e seus derivados, consegue-se uma compreensão melhor das formas e do espaço que as contém. Aumenta-se a perspectiva do mundo plano e espacial, bem como, aumenta o raciocínio lógico-matemático.
Conhecer a matemática, sua história e suas aplicações, com certeza ajuda-nos no entendimento do mundo que nos cerca e nos torna seres pensantes e capazes de solucionar problemas tanto no campo real quanto no imaginário.
“Deus Criou um Mundo Matematicamente Perfeito”.
Robison Sá.
Referência Bibliográfica:
http://www.ipem.sp.gov.br/5mt/unidade.asp?vpro=historia
Texto originalmente publicado em https://www.infoescola.com/matematica/unidades-de-medidas-de-comprimento/