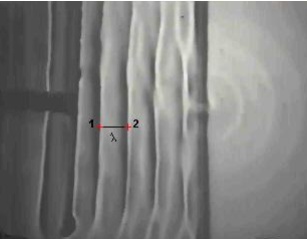
Denomina-se difração o desvio sofrido por ondas ao passarem por um obstáculo, tal como as bordas de uma fenda em um anteparo. Pode-se ver a difração da luz, por exemplo, olhando-se para uma fonte luminosa distante, tal como um anúncio de néon através da fenda formada entre dois dedos, ou observando a luz que escoa pelo tecido de um guarda-chuva. Em geral os efeitos de difração são muito pequenos, devendo ser analisados e investigados minuciosamente.
Além disso a maioria das fontes de luz são corpos extensos, de modo que a forma da figura de difração produzida por um dos pontos da fonte se superporá à das outras.
Finalmente, a maioria das fontes luminosas são ordinárias não monocromáticas, de modo que os espectros de vários comprimentos de onda se superporão e, uma vez mais, seu efeito se tornará menos evidente.
A difração foi descoberta por Francesco Maria Grimaldi (1618-1663), sendo um fenômeno conhecido por Newton (1642-1727) que não foi capaz de reconhecer nenhuma justificativa para a teoria ondulatória da luz neste fato, sendo que este fato poderia ter sido melhor investigado, já Huygens (1629-1695) que não acreditava na teoria da difração, e sim acreditava que suas ondas secundárias só agiam efetivamente no ponto de tangência com a envolvente comum, negado, pois a possibilidade de haver a difração em suas próprias palavras:
“ E assim, vemos as razões pelas quais a luz... se propaga somente em linha reta, de modo que não ilumina nenhum objeto, a menos que esteja num percurso retilíneo com a fonte.”
Fresnel (1788-1827) usou corretamente a princípio de Huygens para explicar a difração. Naqueles tempos, supunha-se que a luz consistia de ondas mecânicas, produzidas em um éter onipresente. Como Maxwell mostrou que a natureza das ondas luminosas não era mecânica, mas, sim eletromagnética. Einstein (1879-1955) chegou à concepção moderna dessas ondas, eliminando a necessidade do éter.
Difração por uma fenda única
Sendo uma fenda de largura a, dividida em N trechos de extensão x. Cada um dos trechos age como um irradiador das ondas secundárias de Huygens, produzindo a perturbação ondulatória característica, no ponto P, cuja posição no anteparo pode ser expressa em função do ângulo θ, para cada disposição do conjunto.
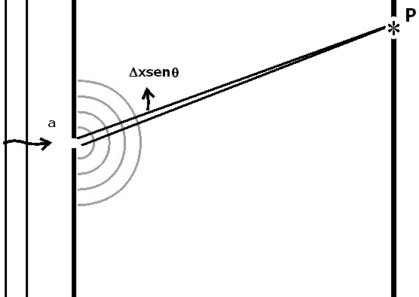
As perturbações ondulatórias, provenientes das faixas adjacentes, apresentam em P uma diferença de fase que será constante  .
.
Onde:

Lembrando que a difração ocorre com qualquer tipo de onda, eletromagnéticas ou mecânicas.
Texto originalmente publicado em https://www.infoescola.com/fisica/difracao/