Mecânica Lagrangeana

A formulação da mecânica clássica postulada por Joseph-Louis de Lagrange relaciona a conservação de energia mecânica com a conservação do momento linear de um sistema dinâmico. É antecessora às formulações das mecânicas hamiltoniana e newtoniana, sendo assim, considerada de fundamental importância a estas.

Função Lagrangeana

A função de Lagrange pode ser definida por:

$L(r, \dot{r}, t) = T(r, \dot{r}, t) - U(r)$

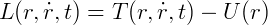
Assim, Lagrangeana (uma função de coordenadas) é igual à diferença entre as energias cinética (T) e potencial (U) de uma partícula em movimento, levando-se em consideração a taxa de variação das coordenadas generalizadas, das velocidades generalizadas da partícula e do tempo: apenas a energia potencial é unidimensional, sendo esta baseada nas coordenadas de posição da partícula.

Lagrange e o Princípio de Hamilton

A mecânica Hamiltoniana defende que dentre os diversos caminhos que um sistema dinâmico dispõe para realizar movimento entre dois pontos, será escolhido espontaneamente àquele que torna menor a diferença entre as energias cinética e potencial. De modo que:

$\delta \int (T - U) dt = 0$

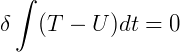
Desse princípio Hamiltoniano, obtêm-se as equações diferenciais parciais de segunda ordem em t de Euler-Lagrange:

$\frac{\partial L}{\partial q_i} - \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{q}_i}\right) =0$

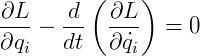
Dessas equações diferenciais parciais, conclui-se que, num sistema conservativo, a diferença entre as Lagrangeanas de dois pontos consecutivos em relação ao tempo é nula. Portanto, as perdas energéticas também são.

Para um sistema não conservativo (dissipativo), vale o seguinte:

$\frac{\partial L}{\partial q_i} - \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{q}_i} \right) = -Q^{ext}_i$

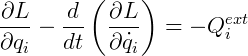
Nesse caso, a diferenças entre as Lagrangeanas é igual ao trabalho realizado pelas forças generalizadas que agem sobre a partícula a determinadas distâncias. Distâncias essas, também representadas por coordenadas n-dimensionais:

$Q^{ext}_i = \sum\limits_{j}^{N} \vec{F}^{ext}_j \cdot \frac{\partial \vec{r}_j}{\partial q_i}$

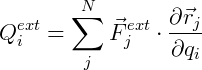
Sendo 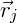$\vec{r}_j$ = vetor que representa a posição da partícula, e 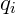$q_i$  = coordenadas n-dimensionais da partícula.

Conservação do Momento Linear

A mecânica Lagrangeana (por possuir um sistema de coordenadas mais geral do que a mecânica newtoniana, por exemplo) consegue resolver problemas mais complexos e discrimina fenômenos que podem atingir velocidades relativísticas (velocidades muito altas) com igual precisão daqueles com velocidades mais baixas.

Considerando o espaço totalmente homogêneo e conservativo, e que as coordenadas generalizadas são apenas em função de uma dimensão espacial (representada por um único módulo do vetor posição r), tem-se que:

$\frac{\partial L}{\partial r} = 0$

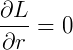
Sendo as perdas energéticas iguais a zero, pelas equações de Euler-Lagrange:

$\frac{d}{dt} \left(\frac{\partial L}{\partial \dot{r}} \right) = 0$

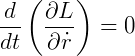
E, ainda, considerando o movimento linear de uma partícula igual a p, sendo este igual a:

$p = \frac{\partial L}{\partial \dot{r}}$

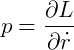
Substituindo na segunda equação, tem-se:

$\frac{dp}{dt} = 0$

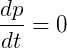
Sendo assim, a quantidade de movimento de uma partícula não varia no tempo se a mesma estiver contida num espaço homogêneo e conservativo.

Fontes:
http://pt.wikipedia.org/wiki/Mecânica_lagrangeana (acesso em 01/04/2010)
http://200.145.134.134/twiki/pub/Main/DisciplinaClassica/hamilton.pdf (acesso em 01/04/2010)

Texto originalmente publicado em https://www.infoescola.com/fisica/mecanica-lagrangeana/