A vergência (C) de uma lente é o inverso da distância focal da mesma. Ou seja:
E sendo a distância focal dada em metros, a vergência é o inverso: m-1. A unidade equivalente ao inverso do metro é a dioptria (SI), entretanto, cotidianamente a medida mais utilizada coloquialmente é o grau. Assim, o grau ou dioptria de uma lente é maior tanto quanto for menor a sua distância focal.
Foco de uma Lente
Observe os seguintes esquemas:
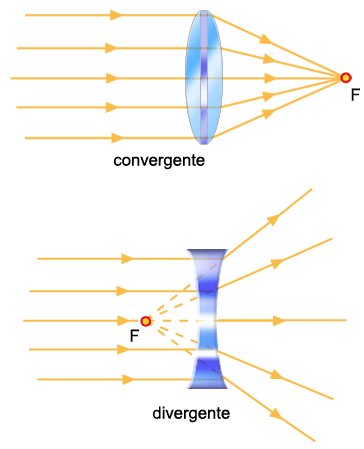Na lente convergente os raios de luz refratados convergem para um ponto em comum, assim como os prolongamentos dos feixes refratados numa lente divergente.
É esse ponto de convergência que se denomina foco: ponto para o qual todos os feixes refratados, ou os seus prolongamentos, convergem e formam a imagem de um objeto. Sendo que, numa lente convergente o foco encontra-se após a lente – sistematicamente a posição da imagem assume sinal negativo, é uma imagem real -, e numa lente divergente o foco se localiza antes da lente – posição da imagem positiva, assim é considerada uma imagem virtual.
Equação dos Fabricantes de Lentes
A partir da equação originária de um sistema de imagem formada por um dioptro esférico por demonstração geométrica e matemática:
Pode-se adaptar a equação para uma lente formada por dois dióptros, sendo:
Dividindo-se todos os membros pelo índice de refração do meio 1:
Lembrando-se que:
Obtém-se a equação dos fabricantes de lentes:
Onde , assim é definido o cálculo da dioptria de uma lente levando-se em consideração os raios de curvatura dos dióptros e dos índices de refração da lente e do meio.
Texto originalmente publicado em https://www.infoescola.com/fisica/vergencia/