Conteúdo deste artigo
Cubo
Cubo é um prisma regular limitado por 6 quadrados congruentes.
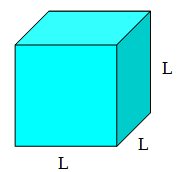
Cubo de aresta medindo L, ou seja, todas as faces são quadrados cujos lados medem L.
Área externa do cubo
Considerando um cubo de aresta medindo L, cada uma das suas faces (quadrados de lado medindo L) possuem área igual a L²:
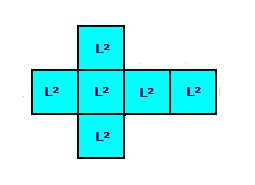
Portanto, a área externa (ou área total) do cubo é dada por:
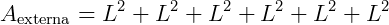
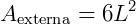
Diagonal de um cubo
Sabemos que o diagonal de um quadrado de medida L é 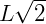 :
:
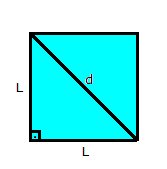
Pelo Teorema de Pitágoras:
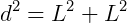
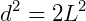
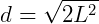
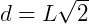
A diagonal do cubo (D) é, em consequência, obtida por:
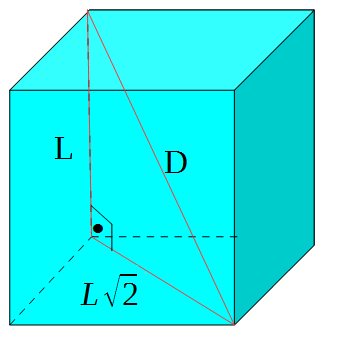
Também pelo Teorema de Pitágoras:
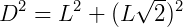
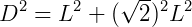
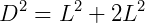
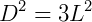
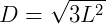
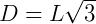
Portanto, a diagonal de um cubo de lado L é dada por: 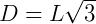
Volume do cubo
No texto volume do prisma, vemos que o volume de um prisma é dado por: 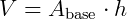 , onde é
, onde é  a área da base e h é a altura.
a área da base e h é a altura.
No caso do cubo, a base (como todas as faces) é um quadrado de lado L, logo, tem área igual a L². A altura será também L. Portanto, o volume do cubo é L³, pois:
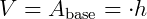
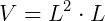
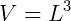
Paralelepípedo
O paralelepípedo é um prisma cuja base é um paralelogramo. No caso de um paralelepípedo reto, o mais importante, temos que o paralelogramo da base é um retângulo:
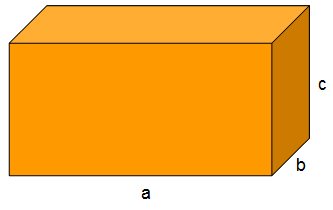
Paralelepípedo reto de medidas a, b e c.
Área externa de um paralelepípedo reto
Sabendo que a área de um retângulo de lados a e b é ab, ou seja, a vezes b, podemos calcular a área externa de um paralelepípedo reto da seguinte maneira:
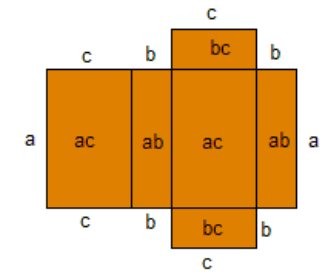
Logo, a área externa (ou total) de um paralelepípedo reto é dada por:
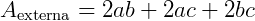
Volume do paralelepípedo
No texto volume do prisma, vemos que o volume de um prisma é dado por: 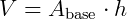 , onde é
, onde é  a área da base e h é a altura.
a área da base e h é a altura.
No exemplo acima, a base é um retângulo de lados a e b, logo, tem área igual a ab e a altura mede c. Portanto, o volume do paralelepípedo é abc, pois:
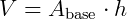
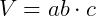
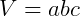
Texto originalmente publicado em https://www.infoescola.com/geometria-espacial/cubo-e-paralelepipedo/