O Volume de um prisma é dado pela multiplicação da área da base (Ab) vezes a altura (h):
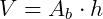
Abaixo, justificamos essa expressão:
Em matemática, princípio tem a ideia de “ponto de partida”, o início de determinado estudo. Para entendermos a forma de cálculo do volume de um prisma, recorremos ao Princípio de Cavalieri:
Princípio de Cavalieri
As definições de cilindro e prisma têm algo em comum: ambas retratam sólidos geométricos com bases paralelas e congruentes. Sabendo disso, suponha que exista um cilindro e um paralelepípedo (prisma) com mesma altura (h).
Sendo A1 e A2 as áreas das bases do cilindro e do paralelepípedo, respectivamente.
Suponha também que A1 = A2,ou seja, que a área das bases também sejam iguais (assim como a altura h).
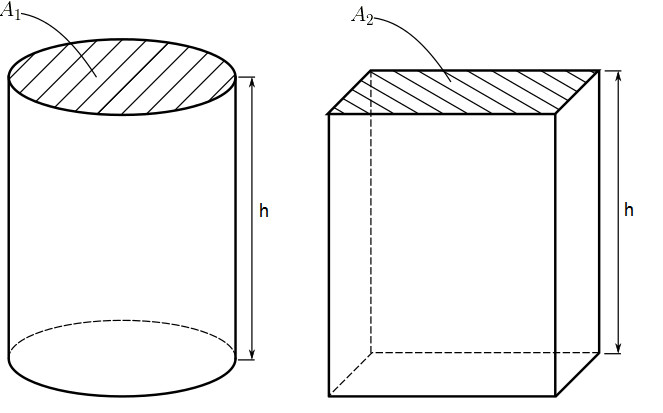
O Matemático Italiano Francesco Bonaventura Cavalieri (1598-1647) observou que, nessas condições, os sólidos (o cilindro e o paralelepípedo) têm o mesmo volume.
Tal princípio nos traz que o prisma e o cilindro podem ser pensados como união de h camadas (polígonos e círculos, respectivamente) de áreas iguais. Tudo isso porque juntando esses polígonos ou círculos (figuras 2D), um em cima do outro de determinado modo, formamos um sólido (figura 3D). Os polígonos formarão os prismas e os círculos formarão os cilindros.
É por esse pensamento, então, que deduzimos que o volume do prisma e do cilindro podem ser obtidos pela área da base (camada) vezes altura (o número de camadas).
Veja mais em:
Um grupo ligado a Universidade de Campinas (UNICAMP), chamado Matemática interativa, criou um vídeo muito interessante e divertido explicando o princípio de Cavalieri.
O vídeo está disponível no YouTube: https://www.youtube.com/watch?v=2pP9aR4nkQc
Mais detalhes e objetos do Matemática Multimídia em: http://m3.ime.unicamp.br/
Texto originalmente publicado em https://www.infoescola.com/matematica/volume-do-prisma/