Prisma é um poliedro cujas bases são duas regiões poligonais congruentes (mesma forma e mesmo tamanho) e paralelas. Suas faces laterais são regiões em forma de paralelogramo.
Conteúdo deste artigo
Nomenclatura de Prismas
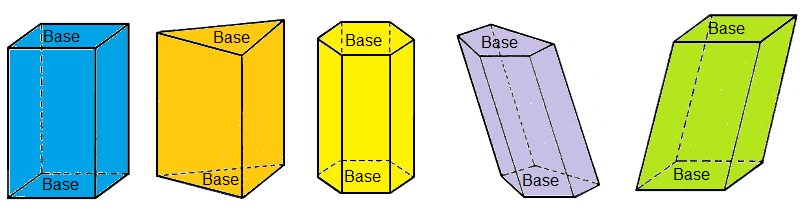
A nomenclatura de prisma ocorre de acordo com o polígono de suas bases. Alguns exemplos:
- Prisma triangular: bases são triângulos.
- Prisma quadrangular: bases são quadrados.
- Prisma pentagonal: bases são pentágonos.
- Prisma hexagonal: bases são hexágonos.
- Prisma heptagonal: bases são heptágonos.
- Prisma octogonal: bases são octógonos.
Elementos do prisma
- Bases: são as faces paralelas e congruentes do prisma.
- Faces laterais: são todas paralelogramos. No caso de um prisma reto, as faces laterais são retângulos.
- Altura (h): é a menor distância entre as suas bases.
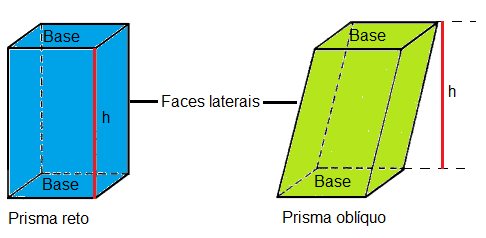
Observação: No caso do prisma reto, a altura coincide com a medida da aresta lateral. Já no caso do prisma oblíquo, a altura não é paralela à aresta lateral.
Classificação de prismas
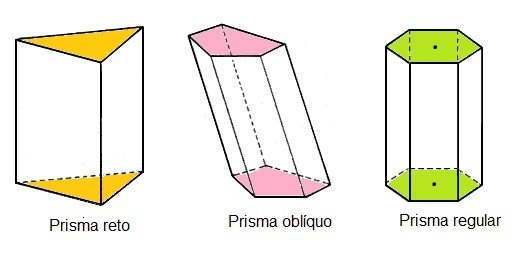
- Prisma reto: As arestas laterais formam um ângulo reto (90°) com as bases.
- Prisma oblíquo: As arestas laterais formam um ângulo diferente de 90° com as bases
- Prisma regular: é um prisma reto e sua base é um polígono regular.
Observação: um polígono é regular se, e somente se, todos os seus lados possuem a mesma medida e todos os ângulos internos são congruentes entre si.
Leia também:
Texto originalmente publicado em https://www.infoescola.com/geometria-espacial/prisma/