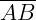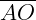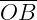Conteúdo deste artigo
Círculo e circunferência
Vamos definir primeiro o que é uma circunferência.
Circunferência é a figura geométrica formada por todos os pontos que equidistam de um ponto fixo, chamado de centro.
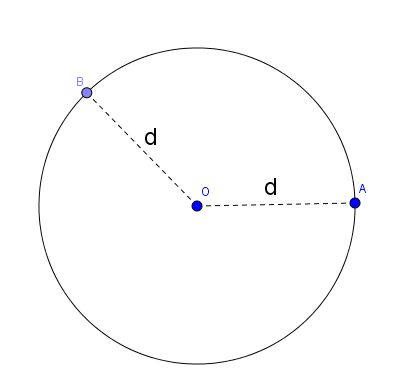
Assim, todos os pontos da circunferência têm a mesma distância ao centro. A distância do ponto A até o centro, por exemplo, é a mesma entre o ponto B e o centro.
Podemos definir um círculo como sendo o conjunto de todos os pontos interiores de uma circunferência, ou seja, é o espaço contido dentro da circunferência.
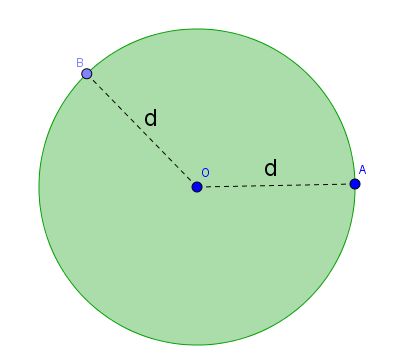
Assim, fica claro que:
- Circunferência: apenas a “linha” exterior.
- Círculo: circunferência mais o que está dentro dela.
Assim, quando calculamos a área, estamos falando de círculo e não de circunferência.
Todo círculo ou circunferência possui alguns elementos importantes:
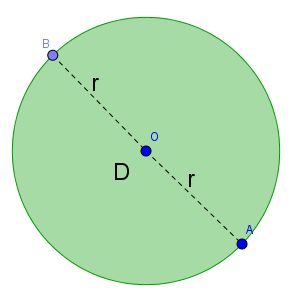
- O é o centro da circunferência;
 é o Diâmetro (D);
é o Diâmetro (D); e
e  são raios (r);
são raios (r);
Podemos estabelecer a seguintes relações:
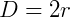
Diâmetro é o dobro do raio, ou:
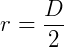
O raio é metade do diâmetro.
Essas considerações são importantes no momento da resolução de algum exercício, na maioria das vezes.
Área de um círculo
A área de um círculo pode ser determinada matematicamente por:
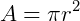
Onde r é a medida do círculo e 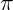 um valor constante e usualmente igual a 3,14.
um valor constante e usualmente igual a 3,14.
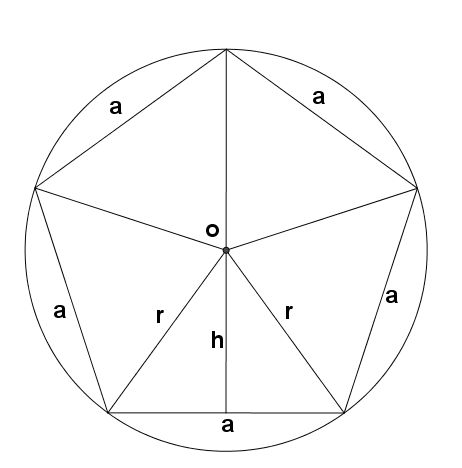
Para compreendermos um pouco de onde obtemos essa fórmula, vamos imaginar uma circunferência qualquer e alguns polígonos dentro dela.
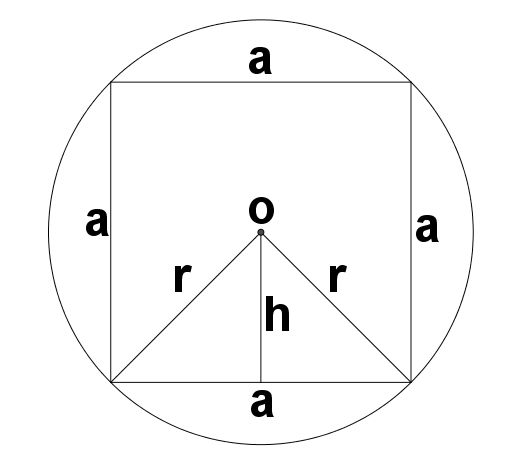
Para determinar a área do quadrado dentro da figura acima, vamos calcular a área do triângulo de base a e altura h:
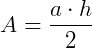
Como o quadrado é composto por 4 triângulos iguais, a sua área será:
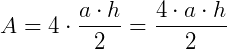
(Note que 4.a equivale ao perímetro do quadrado)
Utilizando o mesmo processo, a área do triângulo será:
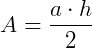
Como temos 5 triângulos, teremos: 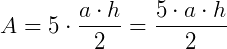 .
.
Novamente note que 5.a equivale ao perímetro do pentágono.
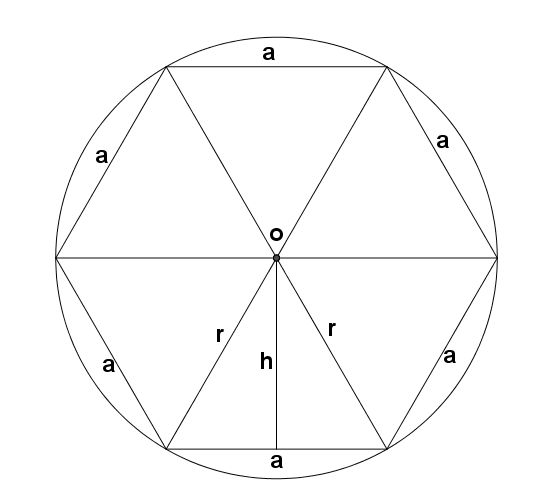
Novamente a área do triângulo 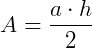 será e a área do hexágono será
será e a área do hexágono será 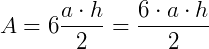 .
.
Observe que quanto maior a quantidade de lados que o polígono tiver, mais ele estará se aproximando de um círculo. Veja como ficaria um polígono de 10 lados.
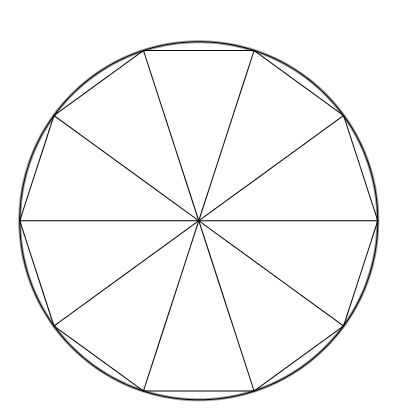
Em todos esses casos, a área do polígono será 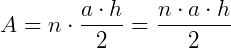 .
.
Sendo n a quantidade de lados do polígono e n . a o perímetro desse polígono.
gora vamos imaginar um polígono de n lados. A quantidade de lados é tão grande que mal podemos visualizá-los. Imaginemos que esse polígono seja o próprio círculo.
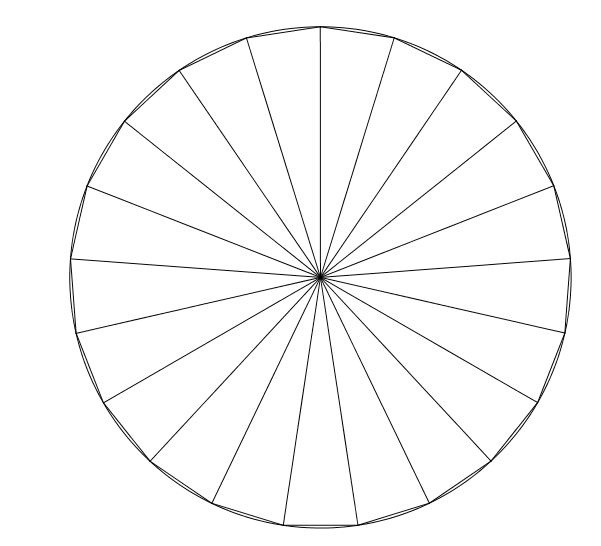
Vamos calcular a área, então, desse polígono que estamos enxergando como um círculo, já que a quantidade de lados é tão pequena que mal podemos enxergá-los.
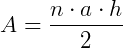
Como se trata agora de um círculo, a altura h será o raio r. o perímetro agora, n . a, será o comprimento de uma circunferência, então 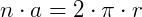 .
.
Substituindo teremos:
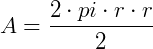
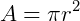
Portanto, fica demonstrada a fórmula para o cálculo da área de um círculo.
De onde veio  ?
?
O valor de 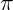 é obtido quando dividimos o comprimento da circunferência pelo seu diâmetro. Assim, em qualquer circunferência, quando dividimos o comprimento pelo diâmetro, obteremos o valor de
é obtido quando dividimos o comprimento da circunferência pelo seu diâmetro. Assim, em qualquer circunferência, quando dividimos o comprimento pelo diâmetro, obteremos o valor de 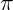 .
.
Exemplos:
1 – “Calcule a área de um círculo cujo diâmetro mede 20 cm”
Como vimos nas relações entre raio e diâmetro, o raio é metade do diâmetro e o diâmetro é o dobro do raio. Para utilizar a fórmula do cálculo da área do círculo precisamos do valor do raio. Como o diâmetro mede 20 cm, o raio será metade dessa medida, ou seja, 10 cm.
Aplicando a fórmula, teremos:
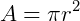
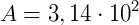
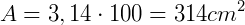
2 – “Considerando que uma pizza tradicional grande possui 35 cm de raio e uma pizza tradicional pequena apresenta 25 cm, determine a diferença entre a área das duas pizzas. ”
Vamos calcular as áreas dos dois tipos de pizza.
Pizza grande com 35 cm de raio:
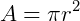
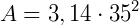
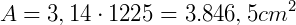
Pizza pequena com 25 cm de raio
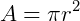
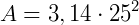
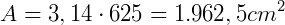
A diferença entre elas será:
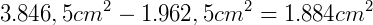
Referências:
DANTE, Luiz Roberto. Matemática: contexto & aplicações. 2. ed. São Paulo: Ática, 2013.
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.
Texto originalmente publicado em https://www.infoescola.com/matematica/area-de-um-circulo/