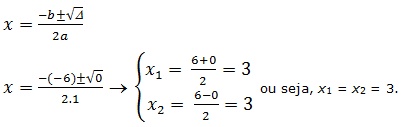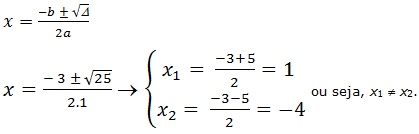Discriminante

São vários os momentos em matemática, bem como em outras áreas do conhecimento, que a evolução do problema em resolução acaba desembocando em equações de 2º grau ou em funções polinomiais de 2º grau (funções quadráticas). Por este motivo, o conhecimento dos processos de resolução desse tipo de equação é importante e, além disso, necessário.

Muitos povos contribuíram para a descoberta e aperfeiçoamento da resolução de equações de grau 2, a exemplo dos árabes, hindus e babilônios. Para se ter uma ideia da idade histórica desses problemas, há aproximadamente 2000 a.C. os babilônios já conheciam e resolviam equações de 2º grau, em parte dos casos com a ajuda de figuras geométricas.

Este trabalho trata, prioritariamente, do discriminante encontrado na fórmula resolutiva, conhecida também por fórmula de Bhaskara, suas particularidades e operacionalidades.

O discriminante (Δ)

A fórmula resolutiva para equações completas e incompletas do 2º grau é 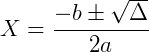$X = \frac{-b \pm \sqrt{\Delta}}{2a}$, onde $\Delta = b^{2} - 4ac$.

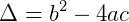O discriminante, representado pela letra grega Δ (lê-se “delta”) corresponde ao radicando da fórmula resolutiva e tem o valor do coeficiente b elevado à segunda potência, menos o produto de quatro pelos coeficientes a e c.

Coeficientes são números reais que acompanham as incógnitas, no caso de a e b, ou é independe das incógnitas, no caso de c.

A representação geral de uma equação de 2º grau é:

ax² + bx + c = 0, com a ≠ 0.

Particularidades de Δ

Algumas peculiaridades do discriminante merecem atenção. Veja cada uma delas:

1. Δ = 0. Quando o discriminante é igual à zero a equação de 2º grau apresenta duas raízes reais iguais.

Ex.: Resolva a equação x² – 6x + 9 = 0.

Separando os coeficientes

a = 1, b = – 6 e c = 9.

Calculando o valor do discriminante

Δ = b² – 4ac

Δ = (– 6)² – 4.1.9

Δ = 36 – 36

Δ = 0

x² – 6x + 9 = 0

2. Δ > 0. Quando o valor do discriminante é maior que zero, a equação apresenta duas raízes reais diferentes.

Ex.: Resolva a equação x² + 3x – 4 = 0.

Separando os coeficientes

a = 1, b = 3 e c = – 4.

Calculando o valor do discriminante

Δ = b² – 4ac

Δ = (3)² – 4.1.(– 4)

Δ = 9 – 16

Δ = 25

x² + 3x – 4 = 0

3.  Δ < 0. Quando o discriminante é menor que zero, não existem raízes reais (em R).

Ex.: Determine o conjunto solução da equação quadrática x² + 5x + 7 = 0.

Separando os coeficientes

a = 1, b = 5 e c = 7.

Calculando o valor do discriminante

Δ = b² – 4ac

Δ = 5² – 4.1.(7)

Δ = 25 – 28

Δ = – 3

x² + 5x + 7 = 0

Portanto, o conjunto solução desta equação é: 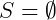$S=\emptyset$.

“Nem todos os caminhos que levam ao sucesso são fáceis.”

(Robison Sá)

Referência bibliográfica:
BIANCHINI, Edwaldo. Matemática, 9º ano. – 7. ed. – São Paulo: Moderna, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/discriminante/