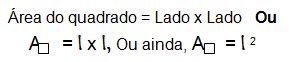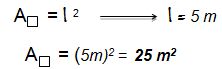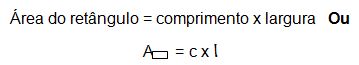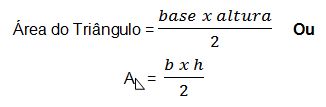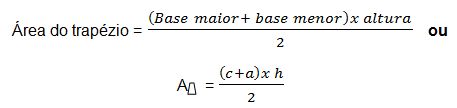Nesse estudo sobre a Geometria Euclidiana ou Plana, serão abordados os principais conceitos e um pouco da história desse ramo da matemática milenar que desempenha tão grande representatividade na vida da humanidade. Não há dúvidas da importância da Geometria na vida humana. O conhecimento geométrico revolucionou o saber, tornando-se o seu estudo, necessário à realização de grandes feitos nas áreas da construção e na partilha de terras. Se dividirmos a palavra Geometria conseguimos chegar ao seu significado etimológico: geo (terra) + metria (medida), portanto Geometria significa medida de terra.
Conteúdo deste artigo
Passeio pela História
O conhecimento geométrico como conhecemos hoje nem sempre foi assim. A geometria surgiu de forma intuitiva, e como todos os ramos do conhecimento, nasceu da necessidade e da observação humana. O seu início se deu forma natural através da observação do homem à natureza. Ao arremessar uma pedra num lago, por exemplo, observou-se que ao haver contato dela com a água, formavam-se circunferências concêntricas – centros na mesma origem. Para designar esse tipo de acontecimento surgiu a Geometria Subconsciente.
Conhecimentos geométricos também foram necessários aos sacerdotes. Por serem os coletores de impostos da época, a eles era incumbida a demarcação das terras que eram devastadas pelas enchentes do Rio Nilo. A partilha da terra era feita diretamente proporcional aos impostos pagos. Enraizada nessa necessidade puramente humana, nasceu o cálculo de área.
Muitos acontecimentos se deram, ainda no campo da Geometria Subconsciente, até que a mente humana fosse capaz de absorver propriedades das formas antes vistas intuitivamente. Nasce com esse feito a Geometria Científica ou Ocidental. Essa geometria, vista nas instituições de ensino, incorpora uma série de regras e sequências lógicas responsáveis pelas suas definições e resoluções de problemas de cunho geométrico.
Foi em 300 a.C. que o grande geômetra Euclides de Alexandria desenvolveu grandiosos trabalhos matemático-geométricos e os publicou em sua obra intitulada Os Elementos. Essa foi, e continua sendo, a maior obra já publicada - desse ramo - de toda a história da humanidade. A Geometria plana, como é popularmente conhecida nos dias atuais, leva também o título de Geometria Euclidiana em homenagem ao seu grande mentor Euclides de Alexandria.
Cálculo de Áreas
Conhecer sobre área é conhecer sobre o espaço que podemos preencher em regiões poligonais convexas – qualquer segmento de reta com extremidades na região só terá pontos pertencentes a esta.
O cálculo de áreas tem muita aplicabilidade em diferentes momentos, seja em atividades puramente cognitivas, ou até mesmo trabalhistas. Um exemplo de profissional que faz uso dessa ferramenta para tornar possível o desempenho do seu trabalho é o pedreiro. É através do conhecimento de área que é possível estimar a quantidade de cerâmica necessária para pavimentar um determinado cômodo de uma casa, por exemplo.
O quadrado
O quadrado é uma figura geométrica plana regular em que todos os seus lados e ângulos são iguais. Veja um exemplo de quadrado na figura a seguir:
Para calcular a área de um quadrado basta que se multipliquem dois dos seus lados l entre si.
Exemplo 1
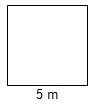Para pavimentar a sala de sua casa D. Carmem comprou 26 m2 de piso. Sabendo que a sala tem o formato quadrangular e que um dos lados mede 5 m, diga se o piso comprado por D. Carmem será suficiente para pavimentar a sua sala.
- A sala tem o formato quadrangular;
- O seu lado mede 5 m;
- A área do quadrado é A = l 2.
Com base nos dados acima temos:
Conclui-se então que o piso comprado por D. Carmem será suficiente para pavimentar sua sala e ainda sobrará 1 m2.
Lembrete: a unidade de medida de área mais utilizada é o metro quadrado (m2), porém em alguns casos usa-se o km2, cm2, etc.
O retângulo
O retângulo é uma figura geométrica plana cujos lados opostos são paralelos e iguais e todos os ângulos medem 90º. Confiram o retângulo abaixo:
Para calcular a área do retângulo, basta que se multipliquem seu comprimento c pela largura l.
Exemplo 2
Num campeonato de futebol a equipe organizadora do evento está providenciando o gramado que será plantado em toda área do campo. Para comprar as gramas, a equipe precisa saber a área do campo, pois a grama é vendida por metro quadrado. Sabendo que o campo tem 115 m de comprimento por 75 m de largura e ainda que o campo tem o formato retangular, ajude a equipe a solucionar o problema, diga quantos metros quadrados de área tem o campo de futebol?
O triângulo
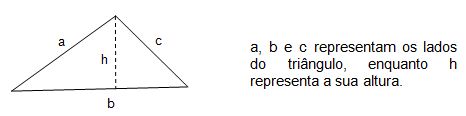
O triângulo é uma figura geométrica plana formada por três lados e três ângulos. A soma dos seus ângulos internos é igual 180º.
Para calcular a área do triângulo multiplica-se a base b pela altura h e divide o resultado por 2 (metade da área do retângulo).
Exemplo 3
Encontre a área de um triângulo cuja base mede 8,2 cm e a altura 3,6 cm.
O trapézio
O trapézio é uma figura plana com um par de lados paralelos (bases) e um par de lados concorrentes.
Para calcular a área do trapézio adiciona-se a base maior c à base menor a, ao resultado da soma multiplica-se a altura, e por fim, divide-se o resultado final por 2.
Exemplo 4
Um fazendeiro quer saber a área de um lote de terra que acabara de comprar. O lote tem o formato de um trapézio. Sabendo que a frente mede 1020 m, o fundo, 815 m e a distância da frente ao fundo é de 510 m. Determine a área do lote.
Conclusão
A necessidade geométrica perpassou o tempo e está impregnada em nossas vidas nos dias atuais. O conhecimento da Geometria Plana (Euclidiana) é tão importante que não é possível o caminhar separado da sua prática e do seu entendimento.
“Caminhemos sobre as curvas das formas e encontraremos um universo ainda não desbravado”. Robison Sá.
Referência bibliográfica:
Ferret, Rodrigo Bozi. História e filosofia da matemática. Aracaju: Gráf. UNIT, 2007.
Texto originalmente publicado em https://www.infoescola.com/matematica/geometria-plana-conceitos-historicos-e-calculo-de-areas/