Igualdade de matrizes

No artigo sobre matrizes, introduzimos algumas definições preliminares sobre matrizes, formas gerais e suas representações. Neste, trataremos sobre a igualdade de matrizes. Recordando, a forma geral de uma matriz , pode ser escrita como:

$A=[a_{ij}]_{m\times n}=\begin{bmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn}\end{bmatrix}$

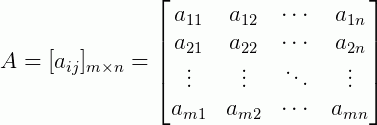
Onde m é o número de linhas e n o número de colunas de uma matriz. Note que o elemento a_ij, também chamado de ij-ésima entrada simboliza a posição deste elemento dentro da matriz, ou seja, a₁₁ está posicionado na 1ª linha e na 1ª coluna. O a₂₁ está na 2ª linha e na 1ª coluna e assim por diante.

Suponha agora duas matrizes A e B, tal que A=B. Dizemos que uma matriz só é igual à outra se, e somente se, ambas tiverem as mesmas dimensões e os seus elementos correspondentes sejam iguais. De modo formal escrevemos:

$[a_{ij}]_{m\times n}=[b_{ij}]_{m\times n}$

$\begin{bmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn}\end{bmatrix}=\begin{bmatrix}b_{11}&b_{12}&\cdots&b_{1n}\\b_{21}&b_{22}&\cdots&b_{2n}\\\vdots&\vdots&\ddots&\vdots\\b_{m1}&b_{m2}&\cdots&b_{mn}\end{bmatrix}$

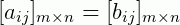
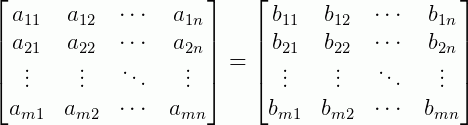
Por exemplo:

$[a_{ij}]_2=[b_{ij}]_2$

$\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}=\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}$

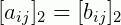
Em outras palavras, podemos dizer que se duas matrizes são iguais então seus elementos obedecem às igualdades: a₁₁=b₁₁, a₁₂=b₁₂, .., a_mn=b_mn. Outro exemplo mais simples: sejam as matrizes:

$A=\begin{bmatrix}1&2&3\\5&-1&4\\-2&0&7\end{bmatrix}$

$B=\begin{bmatrix}1&2&3\\5&-1&4\\-2&0&7\end{bmatrix}$

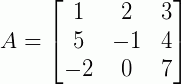
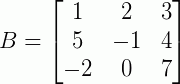
Neste caso, A=B, pois possuem os mesmos elementos e a mesma ordem.

Referências bibliográficas:

ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed. Rio de Janeiro: Elsevier, 2017.

LIPSCHUTZ, Seymor; LIPSON, Marc. Álgebra Linear – 4ª Ed. Porto Alegre: Bookman, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/igualdade-de-matrizes/