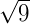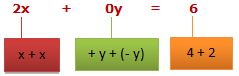Igualdade de matrizes

Ouça este artigo:

Por Robison Sá

O que hoje conhecemos como matriz nasceu de estudos realizados no final do século XVIII com os matemáticos Leibniz, na Alemanha, e Seki Kowa, no Japão. Eles desenvolveram um método de resolução de sistemas lineares baseados em tabelas de números semelhantes às matrizes modernas. Ainda durante todo o século XVIII, matemáticos desenvolveram estudos alicerçados nas propriedades dessas tais tabelas. Pierre Laplace e Alexanre Vandermonde são exemplos deles.

Augustin Cauchy

Todo o desenvolvimento de propriedades e conceituações que utilizamos em dias atuais foram dados no século XX. O matemático Augustin Cauchy, apresentou trabalho primordial sobre essas tabelas do qual derivaram outros importantes trabalhos de matemáticos como Jacobi, Arthur Cayley, James Sylvester e Francisco Brioschi.

Conceituando

Dizemos que duas matrizes A e B de mesma ordem são iguais quando os seus elementos correspondentes são iguais (A = B). Da mesma forma, se essas duas matrizes A e B não têm a mesma ordem ou se seus elementos correspondentes são diferentes, dizemos que elas são matrizes diferentes (A ≠ B).

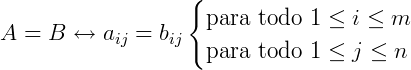
$A = B \leftrightarrow a_{ij} = b_{ij} \begin{cases}\text{para todo } 1 \leq i \leq m\\\text{para todo } 1 \leq j \leq n\end{cases}$

Exemplo 1

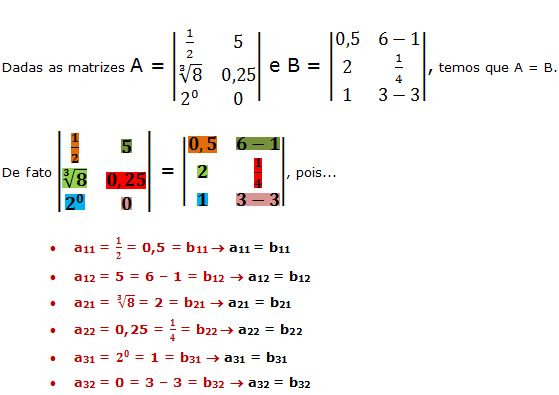
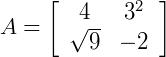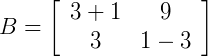As matrizes $A = \left[\begin{array}{cc} 4 & 3^{2} \\ \sqrt{9} & -2 \end{array} \right]$ e $B = \left[\begin{array}{cc} 3+1 & 9 \\ 3 & 1-3\end{array}\right]$ são iguais.

Veja que 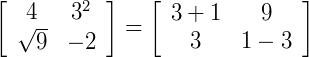$\left[\begin{array}{cc}4 & 3^{2} \\ \sqrt{9} & -2\end{array}\right] = \left[\begin{array}{cc}3+1 & 9 \\ 3 & 1-3\end{array}\right]$ , pois ...

a₁₁ = 4 = 3+1 = b₁₁ → a₁₁ = b₁₁
a₁₂ = 3² = 9 = b₁₂ → a₁₂ = b₁₂
a₂₁ = $\sqrt{9}$ = 3 = b₂₁ → a₂₁ = b₂₁
a₂₂ = -2 = 1-3 = b₂₂ → a₂₂ = b₂₂

Exemplo 2

Aplicando os conceitos

Sabendo os conceitos sobre a igualdade de matrizes vamos resolver uma questão um pouco mais complexa envolvendo esta compreensão. Sempre que for necessário recorra aos exemplos dados anteriormente, como forma de esclarecimento e amenização das dificuldades que surgirem ao longo do caminho.

“A igualdade almejada pelo homem não está no aspecto físico, mas sim na espiritualidade.”

(Robison Sá)

Referências bibliográficas:
SOUZA, Joamir Roberto de. Novo Olhar Matemática. – 1 ed. – São Paulo: FTD, 2010. – (Coleção novo olhar; v. 2)
YOUSSEF, Antonio Nicolau. Matemática: ensino médio, volume único / Antonio Nicolau Youssef, Elizabeth Soares, Vicente Paz Fernandez. – São Paulo: Scipione, 2005.

Texto originalmente publicado em https://www.infoescola.com/matematica/igualdade-de-matrizes/

Conceituando

Aplicando os conceitos