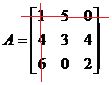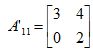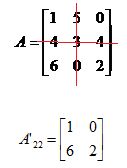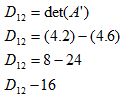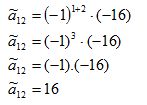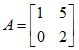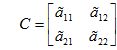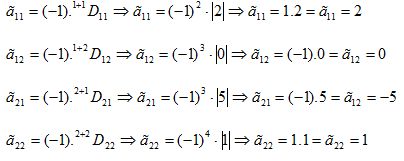Conteúdo deste artigo
Cofatores
Cofator é um número associado a um elemento qualquer de uma matriz quadrada.
Para definir cofator é necessário primeiro definir o menor principal ou menor complementar, associado a um elemento qualquer de uma matriz quadrada.
Menor Principal ou Menor Complementar
Seja a matriz quadrada  , definimos como menor principal (ou complementar) ao determinante da matriz que se obtém eliminando a linha i e a coluna j da matriz A, representamos o menor principal por D.
, definimos como menor principal (ou complementar) ao determinante da matriz que se obtém eliminando a linha i e a coluna j da matriz A, representamos o menor principal por D.
Exemplos:
a) Determinar o menor principal D11, associado ao elemento a11.
O menor principal associado ao elemento a11 é a matriz que se obtém eliminando a linha e a coluna e quem está o elemento a11.
O elemento a11 é o número 1. Eliminando a sua linha e a sua coluna obtemos a matriz A’, associado ao elemento a11, que é a matriz quadrada formada pelos elementos restantes, isto é:
O menor principal será portanto o determinante de A’. Assim, temos que D11 = det(A’)
- Det = (3.2)-(4.0)
- Det = 6 – 0
- Det = 6
E, portanto:
D11 = 6
b) Determinar o menor principal associado ao elemento a22.
O elemento a22 é o número 3. Eliminando a sua linha e a sua coluna obtemos o a matriz A’, elemento a22, que é a matriz quadrada formada pelos elementos restantes, isto é:
Calculando o menor principal, isto é , o determinante de A’ (det (A’)), temos:
- Det = (1.2) – (6.0)
- Det = 2 – 0
- Det = 2.
Portanto, D22 = 2
Cofator associado a um elemento qualquer de uma matriz quadrada
Uma vez definido o menor principal, podemos então definir cofator como segue:
O cofator ãij, associado a um elemento aij é definido por ![]()
Exemplos:
Considerando a matriz 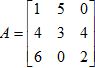 , vamos determinar o cofator associado ao elemento a12.
, vamos determinar o cofator associado ao elemento a12.
Pela definição temos:
Calculando o menor principal (menor complementar) D12, temos:
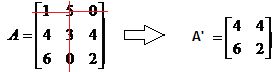
O elemento a12 é o número 5 da matriz A, vamos eliminar a sua linha e a sua coluna, obtendo o menor principal a seguir:
Substituído o menor principal D12 na definição temos:
Portanto o cofator de a12, é:
ã12 = 16
Matriz de cofatores
Chamamos de matriz dos cofatores, e representamos por C a matriz formada por todos os cofatores de uma matriz original A.
Exemplo:
Seja A a matriz original dada a seguir:
Vamos determinar a matriz dos “C” de cofatores associada a matriz original A.
A matriz C, dos cofatores pode ser escrita como segue:
Precisamos, portanto, calcular os cofatores ã11, ã12, ã21, ã22, associados aos elementos a11, a12, a21, a22, respectivamente.
Calculando os cofatores, obtemos:
Portanto a matriz C, dos cofatores associados a matriz original A será:
Os cofatores são utilizados para o cálculo do determinante de uma matriz quadrada, enquanto que a matriz de cofatores é utilizada no processo de inversão de matrizes quando utilizamos o método de inversão por matriz adjunta.
Texto originalmente publicado em https://www.infoescola.com/matematica/matriz-de-cofatores/