Matriz transposta

A transposta de uma matriz (ou matriz transposta) é aquela que é obtida quando escrevemos as colunas de uma matriz, na mesma ordem, como uma linha. De uma maneira simples: O que é linha se torna coluna e o que é coluna se torna linha. Formalmente escrevemos:

$A=[a_{ij}]_{m\times n}\rightarrow A^T=[a_{ji}]_{n\times m}$

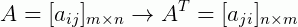
Onde a operação de transposição da matriz A é simbolizada por A^T. Por exemplo:

$A=\begin{bmatrix}2&1\\-3&4\\5&2\end{bmatrix}\rightarrow A^T=\begin{bmatrix}2&-3&5\\1&4&2\end{bmatrix}$

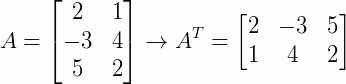
Em alguns livros é comum encontrar esta forma de escrever a transposta de uma matriz da seguinte forma:

$\begin{bmatrix}2&1\\-3&4\\5&2\end{bmatrix}^T=\begin{bmatrix}2&-3&5\\1&4&2\end{bmatrix}$

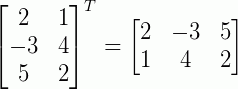
Outro exemplo:

$A=\begin{bmatrix}1&2&3\\5&-1&4\\-2&0&7\end{bmatrix}\rightarrow A^T=\begin{bmatrix}1&5&-2\\2&-1&0\\3&4&7\end{bmatrix}$

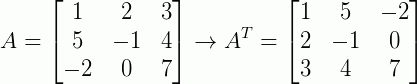
A transposta de uma matriz linha é uma matriz coluna. Isto é:

$A=\begin{bmatrix}1&2&3\end{bmatrix}\rightarrow A^T=\begin{bmatrix}1\\2\\3\end{bmatrix}$

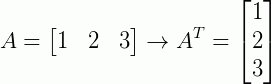
Analogamente, a transposta de uma matriz coluna é uma matriz linha, ou seja:

$A=\begin{bmatrix}1\\2\\3\end{bmatrix}\rightarrow A^T=\begin{bmatrix}1&2&3\end{bmatrix}$

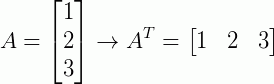
Propriedades importantes

Dadas A e B matrizes quaisquer e x uma constante real, valem as propriedades:

1 - 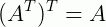$(A^T)^T=A$, que é a transposta da transposta de uma matriz.

𝟐 - 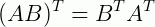$(AB)^T=B^T A^T$, a transposta de um produto é o produto das transpostas, na ordem inversa

3 - 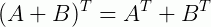$(A+B)^T=A^T + B^T$

4 - 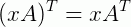$(xA)^T=xA^T$

Referências bibliográficas:

ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed. Rio de Janeiro: Elsevier, 2017.

LIPSCHUTZ, Seymor; LIPSON, Marc. Álgebra Linear – 4ª Ed. Porto Alegre: Bookman, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/matriz-transposta/